수학에서 유클리드 알고리즘은 최대 공약수(GCD)를 계산하는 데 효율적인 방법입니다. 최대공약수는 두 숫자의 나머지를 남기지 않고 두 숫자를 나누는 가장 큰 숫자입니다.
유클리드 알고리즘은 더 큰 숫자가 더 작은 숫자와의 차이로 대체되면 두 숫자의 최대 공약수가 변하지 않는다는 원칙에 기반합니다. 예를 들어 252와 105의 최대공약수는 21(252 = 21 × 12 와 105 = 21 × 5) 이고, 105와 252 - 105 = 147의 최대공약수 역시 21입니다. 이 대체가 두 숫자 중 큰 숫자를 줄이기 때문에이 과정을 반복하면 두 숫자가 동일해질 때까지 작은 숫자 쌍이 연속적으로 제공됩니다. 그 때, 그들은 원래의 두 숫자의 GCD입니다.
단계들을 반대로함으로써, 최대공약수는 양수 또는 음의 정수, 예를 들어, 21 = 5 × 105 + (-2) × 252을 곱한 2 개의 원래 수의 합으로 표현 될 수 있습니다. 이러한 방식으로 최대공약수를 항상 표현할 수 있다는 사실을 Bézout의 정체성이라고합니다.
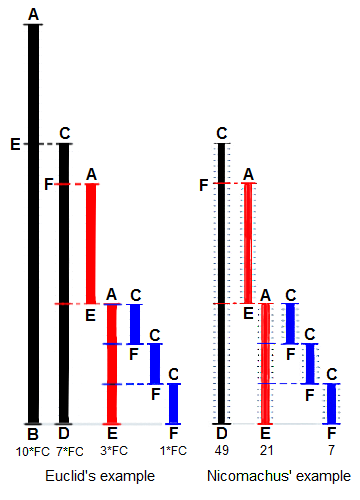
유클리드는 두 개의 시작 길이 인 BA와 DC의 최대 공약수 (GCD)를 찾는 방법으로 둘 다 공통 "단위"길이의 배수로 정의됩니다. DC는 길이가 더 짧고 BA를 채우는 데 사용되지만, 남은 EA가 DC미만이므로 한 번만 사용됩니다. 이제 EA는 더 짧은 길이의 DC를 (두 번) 채우고, 남은 FC는 EA보다 짧습니다. 그러면 FC는 EA를 (3 번) 채웁니다. 나머지가 없으므로 프로세스는 FC가 GCD인 것으로 끝납니다. 오른쪽에 Nicomachus의 '49'와 '21'의 예제는 최대공약수는 7이 나온다. (히스 1908 : 300에서 파생 됨)
24 x 60사각형은 10개의 12 x 12정사각형 타일로 덮여 있으며, 12는 24와 60의 GCD입니다. 보다 일반적으로, a-by-b사각형은 c가 a와 b의 공통 제수 일 경우에만 길이가 c인 정사각형 타일로 덮을 수 있습니다.
유클리드 알고리즘의 뺄셈 기반 애니메이션.
초기 직사각형의 크기는 a = 1071과 b = 462입니다. 462 × 462 크기의 사각형이 그 안에 배치되어 462 × 147 사각형이 남습니다. 이 직사각형은 21 × 147사각형이 남을 때까지 147 × 147정사각형으로 바둑판 식으로 배열되며, 21 × 21정사각형으로 바둑판 식으로 배열되며 덮여지지 않는 영역은 남지 않습니다.
가장 작은 정사각형 크기 인 21은 1071과 462의 GCD입니다.