# 유클리드 알고리즘 수학에서 유클리드 알고리즘은 최대 공약수(GCD)를 계산하는 데 효율적인 방법입니다. 최대공약수는 두 숫자의 나머지를 남기지 않고 두 숫자를 나누는 가장 큰 숫자입니다. 유클리드 알고리즘은 더 큰 숫자가 더 작은 숫자와의 차이로 대체되면 두 숫자의 최대 공약수가 변하지 않는다는 원칙에 기반합니다. 예를 들어 `252`와 `105`의 최대공약수는 `21`(`252 = 21 × 12` 와 `105 = 21 × 5`) 이고, `105`와 `252 - 105 = 147`의 최대공약수 역시 `21`입니다. 이 대체가 두 숫자 중 큰 숫자를 줄이기 때문에이 과정을 반복하면 두 숫자가 동일해질 때까지 작은 숫자 쌍이 연속적으로 제공됩니다. 그 때, 그들은 원래의 두 숫자의 GCD입니다. 단계들을 반대로함으로써, 최대공약수는 양수 또는 음의 정수, 예를 들어, `21 = 5 × 105 + (-2) × 252`을 곱한 2 개의 원래 수의 합으로 표현 될 수 있습니다. 이러한 방식으로 최대공약수를 항상 표현할 수 있다는 사실을 Bézout의 정체성이라고합니다. 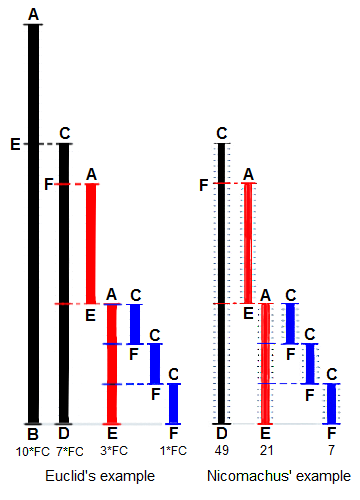 유클리드는 두 개의 시작 길이 인 `BA`와 `DC`의 최대 공약수 (GCD)를 찾는 방법으로 둘 다 공통 "단위"길이의 배수로 정의됩니다. `DC`는 길이가 더 짧고 `BA`를 채우는 데 사용되지만, 남은 `EA`가 `DC`미만이므로 한 번만 사용됩니다. 이제 EA는 더 짧은 길이의 `DC`를 (두 번) 채우고, 남은 `FC`는 `EA`보다 짧습니다. 그러면 `FC`는 `EA`를 (3 번) 채웁니다. 나머지가 없으므로 프로세스는 `FC`가 `GCD`인 것으로 끝납니다. 오른쪽에 Nicomachus의 '49'와 '21'의 예제는 최대공약수는 7이 나온다. (히스 1908 : 300에서 파생 됨)  `24 x 60`사각형은 10개의 `12 x 12`정사각형 타일로 덮여 있으며, `12`는 `24`와 `60`의 GCD입니다. 보다 일반적으로, `a-by-b`사각형은 `c`가 `a`와 `b`의 공통 제수 일 경우에만 길이가 `c`인 정사각형 타일로 덮을 수 있습니다.  유클리드 알고리즘의 뺄셈 기반 애니메이션. 초기 직사각형의 크기는 `a = 1071`과 `b = 462`입니다. `462 × 462` 크기의 사각형이 그 안에 배치되어 `462 × 147` 사각형이 남습니다. 이 직사각형은 `21 × 147`사각형이 남을 때까지 `147 × 147`정사각형으로 바둑판 식으로 배열되며, `21 × 21`정사각형으로 바둑판 식으로 배열되며 덮여지지 않는 영역은 남지 않습니다. 가장 작은 정사각형 크기 인 `21`은 `1071`과 `462`의 GCD입니다. ## 레퍼런스 [Wikipedia](https://en.wikipedia.org/wiki/Euclidean_algorithm)