From 2497cd1bed136b43c5f3bf73a092df5dec50070e Mon Sep 17 00:00:00 2001
From: Jeremy Kang <jeremy.kang@obigo.com>
Date: Fri, 6 Jul 2018 18:34:06 +0900
Subject: [PATCH 1/2] =?UTF-8?q?=EC=A4=91=EA=B0=84=20=EB=B2=88=EC=97=AD=20?=
=?UTF-8?q?=EC=A0=80=EC=9E=A5?=
MIME-Version: 1.0
Content-Type: text/plain; charset=UTF-8
Content-Transfer-Encoding: 8bit
---
README.ko-KR.md | 237 ++++++++++++++++++
.../doubly-linked-list/README.ko-KR.md | 12 +
.../linked-list/README.ko-KR.md | 10 +
src/data-structures/queue/README.ko-KR.md | 12 +
4 files changed, 271 insertions(+)
create mode 100644 README.ko-KR.md
create mode 100644 src/data-structures/doubly-linked-list/README.ko-KR.md
create mode 100644 src/data-structures/linked-list/README.ko-KR.md
create mode 100644 src/data-structures/queue/README.ko-KR.md
diff --git a/README.ko-KR.md b/README.ko-KR.md
new file mode 100644
index 0000000000..b0aa12ce07
--- /dev/null
+++ b/README.ko-KR.md
@@ -0,0 +1,237 @@
+# JavaScript 알고리즘과 자료 구조
+
+[](https://travis-ci.org/trekhleb/javascript-algorithms)
+[](https://codecov.io/gh/trekhleb/javascript-algorithms)
+
+이 저장소에는 자바스크립트 기반의 인기있는 알고리즘과 자료구조를 많이 포함하고 있습니다.
+
+각 알고리즘과 자료구조는 각각 README가 있어서 관련 설명과 (유투브 영상들을 포함한)추가 자료에 대한 링크가 있습니다.
+
+_다른 언어로 보실 수 있습니다:_
+[English](README.md)
+[简体中文](README.zh-CN.md),
+[繁體中文](README.zh-TW.md)
+
+## 자료 구조
+
+자료 구조는 효율적으로 접근하여 수정할 수 있도록 컴퓨터내에 데이터를 구성하고 저장하는 특별한 방법 중 하나입니다. 보다 정확하게는 데이터 구조는 데이터 값의 모음, 데이터 간의 관계 및 데이터에 적용 할 수있는 함수 또는 연산입니다.
+
+`B` - 초심자, `A` - 숙련자
+
+* `B` [Linked List](src/data-structures/linked-list)
+* `B` [Doubly Linked List](src/data-structures/doubly-linked-list)
+* `B` [Queue](src/data-structures/queue)
+* `B` [Stack](src/data-structures/stack)
+* `B` [Hash Table](src/data-structures/hash-table)
+* `B` [Heap](src/data-structures/heap)
+* `B` [Priority Queue](src/data-structures/priority-queue)
+* `A` [Trie](src/data-structures/trie)
+* `A` [Tree](src/data-structures/tree)
+ * `A` [Binary Search Tree](src/data-structures/tree/binary-search-tree)
+ * `A` [AVL Tree](src/data-structures/tree/avl-tree)
+ * `A` [Red-Black Tree](src/data-structures/tree/red-black-tree)
+ * `A` [Segment Tree](src/data-structures/tree/segment-tree) - 최소 / 최대 / 합계 범위 쿼리 예제
+ * `A` [Fenwick Tree](src/data-structures/tree/fenwick-tree) (이진 인덱싱 된 트리)
+* `A` [Graph](src/data-structures/graph) (유향과 무향 모두)
+* `A` [Disjoint Set](src/data-structures/disjoint-set)
+* `A` [Bloom Filter](src/data-structures/bloom-filter)
+
+## 알고리즘
+
+알고리즘은 문제의 클래스를 해결하는 방법에 대한 모호하지 않은 사양입니다. 일련의 작업을 정확하게 정의하는 일련의 규칙입니다.
+
+`B` - 초심자, `A` - 숙련자
+
+### 주제 별 알고리즘
+
+* **수학**
+ * `B` [Bit Manipulation](src/algorithms/math/bits) - set / get / update / clear 비트, 2로 나누기 / 나누기, 네거티브 만들기.
+ * `B` [Factorial](src/algorithms/math/factorial)
+ * `B` [Fibonacci Number](src/algorithms/math/fibonacci)
+ * `B` [Primality Test](src/algorithms/math/primality-test) (시험 분할 방법)
+ * `B` [Euclidean Algorithm](src/algorithms/math/euclidean-algorithm) - 최대 공약수(GCD) 계산
+ * `B` [Least Common Multiple](src/algorithms/math/least-common-multiple) (LCM)
+ * `A` [Integer Partition](src/algorithms/math/integer-partition)
+ * `B` [Sieve of Eratosthenes](src/algorithms/math/sieve-of-eratosthenes) - 주어진 한도까지 모든 소수를 찾는 것
+ * `B` [Is Power of Two](src/algorithms/math/is-power-of-two) - 수치가 2의 거듭 제곱인지 (순진 및 비트 알고리즘)
+ * `A` [Liu Hui π Algorithm](src/algorithms/math/liu-hui) - N-gons에 기초한 대략적인 π 계산
+* **집합**
+ * `B` [Cartesian Product](src/algorithms/sets/cartesian-product) - 여러 세트의 제품
+ * `A` [Power Set](src/algorithms/sets/power-set) - 집합의 모든 하위 집합
+ * `A` [Permutations](src/algorithms/sets/permutations) (반복의 유무)
+ * `A` [Combinations](src/algorithms/sets/combinations) (반복의 유무)
+ * `B` [Fisher–Yates Shuffle](src/algorithms/sets/fisher-yates) - 유한 시퀀스의 무작위 순열
+ * `A` [Longest Common Subsequence](src/algorithms/sets/longest-common-subsequence) (LCS)
+ * `A` [Longest Increasing Subsequence](src/algorithms/sets/longest-increasing-subsequence)
+ * `A` [Shortest Common Supersequence](src/algorithms/sets/shortest-common-supersequence) (SCS)
+ * `A` [Knapsack Problem](src/algorithms/sets/knapsack-problem) - "0/1" and "Unbound" ones
+ * `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray) - "무차별 대입"과 "동적 프로그래밍" (Kadane's) versions
+ * `A` [Combination Sum](src/algorithms/sets/combination-sum) - 특정 합계를 구성하는 모든 조합 찾기
+* **문자열**
+ * `A` [Levenshtein Distance](src/algorithms/string/levenshtein-distance) - 두 시퀀스 간의 최소 편집 거리
+ * `B` [Hamming Distance](src/algorithms/string/hamming-distance) - 심볼이 다른 위치의 수
+ * `A` [Knuth–Morris–Pratt Algorithm](src/algorithms/string/knuth-morris-pratt) (KMP 알고리즘) - 부분 문자열 검색 (패턴 매칭)
+ * `A` [Z Algorithm](src/algorithms/string/z-algorithm) - 부분 문자열 검색 (패턴 매칭)
+ * `A` [Rabin Karp Algorithm](src/algorithms/string/rabin-karp) - 부분 문자열 검색
+ * `A` [Longest Common Substring](src/algorithms/string/longest-common-substring)
+ * `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching)
+* **검색**
+ * `B` [Linear Search](src/algorithms/search/linear-search)
+ * `B` [Binary Search](src/algorithms/search/binary-search)
+* **정렬**
+ * `B` [Bubble Sort](src/algorithms/sorting/bubble-sort)
+ * `B` [Selection Sort](src/algorithms/sorting/selection-sort)
+ * `B` [Insertion Sort](src/algorithms/sorting/insertion-sort)
+ * `B` [Heap Sort](src/algorithms/sorting/heap-sort)
+ * `B` [Merge Sort](src/algorithms/sorting/merge-sort)
+ * `B` [Quicksort](src/algorithms/sorting/quick-sort) - 내부 및 비 내부 구현
+ * `B` [Shellsort](src/algorithms/sorting/shell-sort)
+ * `A` [Counting Sort](src/algorithms/sorting/counting-sort)
+ * `A` [Radix Sort](src/algorithms/sorting/radix-sort)
+* **트리**
+ * `B` [Depth-First Search](src/algorithms/tree/depth-first-search) (DFS)
+ * `B` [Breadth-First Search](src/algorithms/tree/breadth-first-search) (BFS)
+* **그래프**
+ * `B` [Depth-First Search](src/algorithms/graph/depth-first-search) (DFS)
+ * `B` [Breadth-First Search](src/algorithms/graph/breadth-first-search) (BFS)
+ * `A` [Dijkstra Algorithm](src/algorithms/graph/dijkstra) - 모든 그래프 정점에 대한 최단 경로 찾기
+ * `A` [Bellman-Ford Algorithm](src/algorithms/graph/bellman-ford) - 모든 그래프 정점에 대한 최단 경로 찾기
+ * `A` [Detect Cycle](src/algorithms/graph/detect-cycle) - 모든 유향 그래프와 무향 그래프 (DFS 및 분리 세트 기반 버전)
+ * `A` [Prim’s Algorithm](src/algorithms/graph/prim) - 가중 된 무향 그래프에 대한 최소 스패닝 트리 (MST) 찾기
+ * `B` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - 가중 된 무 방향성 그래프에 대한 최소 스패닝 트리 (MST)를 찾는 것.
+ * `A` [Topological Sorting](src/algorithms/graph/topological-sorting) - DFS 방법
+ * `A` [Articulation Points](src/algorithms/graph/articulation-points) - 타잔 알고리즘 (DFS 기반)
+ * `A` [Bridges](src/algorithms/graph/bridges) - DFS 기반 알고리즘
+ * `A` [Eulerian Path and Eulerian Circuit](src/algorithms/graph/eulerian-path) - 벼룩 알고리즘 - 모든 가장자리를 정확히 한 번 방문
+ * `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - 모든 꼭지점을 정확히 한 번 방문
+ * `A` [Strongly Connected Components](src/algorithms/graph/strongly-connected-components) - 코사라줄 알고리즘
+ * `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - 각 도시를 방문하여 출발 도시로 돌아 오는 최단 경로
+* **미분류**
+ * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
+ * `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
+ * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
+
+### 알고리즘 패러다임
+
+알고리즘 패러다임 (algorithmic paradigm)은 알고리즘의 클래스의 디자인의 기초가되는 일반적인 방법 또는 접근법입니다. 알고리즘은 컴퓨터 프로그램보다 높은 추상화와 마찬가지로 알고리즘의 개념보다 높은 추상화입니다.
+
+* **무차별 대입(Brute Force)** - 모든 가능성을 탐색하고 최상의 솔루션을 선택하는 방법
+ * `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
+ * `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - 각 도시를 방문하여 출발 도시로 돌아 오는 최단 경로
+* **탐욕 알고리즘** - 미래에 대한 고려없이 현재 가장 좋은 옵션을 선택하는 방법.
+ * `A` [Unbound Knapsack Problem](src/algorithms/sets/knapsack-problem)
+ * `A` [Dijkstra Algorithm](src/algorithms/graph/dijkstra) - 모든 그래프 정점에 대한 최단 경로 찾기
+ * `A` [Prim’s Algorithm](src/algorithms/graph/prim) - 가중 된 무향 그래프(weighted undirected graph)에 대한 최소 스패닝 트리 (MST) 찾기
+ * `A` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - 가중 된 무향 그래프(weighted undirected graph)에 대한 최소 스패닝 트리 (MST) 찾기
+* **분할 정복** - 문제를 작은 부분으로 나누고 그 부분을 푸는 방법
+ * `B` [Binary Search](src/algorithms/search/binary-search)
+ * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
+ * `B` [Euclidean Algorithm](src/algorithms/math/euclidean-algorithm) - 최대공약수(GCD) 계산법
+ * `A` [Permutations](src/algorithms/sets/permutations) (반복계산 유무)
+ * `A` [Combinations](src/algorithms/sets/combinations) (반복계산 유무)
+ * `B` [Merge Sort](src/algorithms/sorting/merge-sort)
+ * `B` [Quicksort](src/algorithms/sorting/quick-sort)
+ * `B` [Tree Depth-First Search](src/algorithms/tree/depth-first-search) (DFS)
+ * `B` [Graph Depth-First Search](src/algorithms/graph/depth-first-search) (DFS)
+* **동적 프로그래밍** - 이전에 발견 된 하위 해법을 사용하여 해법을 찾는 방법
+ * `B` [Fibonacci Number](src/algorithms/math/fibonacci)
+ * `A` [Levenshtein Distance](src/algorithms/string/levenshtein-distance) - 두 시퀀스 간의 최소 편집 거리
+ * `A` [Longest Common Subsequence](src/algorithms/sets/longest-common-subsequence) (LCS)
+ * `A` [Longest Common Substring](src/algorithms/string/longest-common-substring)
+ * `A` [Longest Increasing subsequence](src/algorithms/sets/longest-increasing-subsequence)
+ * `A` [Shortest Common Supersequence](src/algorithms/sets/shortest-common-supersequence)
+ * `A` [0/1 Knapsack Problem](src/algorithms/sets/knapsack-problem)
+ * `A` [Integer Partition](src/algorithms/math/integer-partition)
+ * `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
+ * `A` [Bellman-Ford Algorithm](src/algorithms/graph/bellman-ford) - 모든 그래프 정점에 대한 최단 경로 찾기
+ * `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching)
+* **역추적** - 무차별 대입법과 마찬가지로 모든 가능한 솔루션을 생성하려고 시도하지만 다음 솔루션을 생성 할 때마다 모든 조건을 충족하는지 테스트 한 다음 후속 솔루션을 계속 생성하십시오. 그렇지 않으면 역 추적하고 솔루션을 찾는 다른 경로로 이동하십시오. 일반적으로 상태 공간의 DFS 통과가 사용됩니다.
+
+ * `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - 모든 꼭지점을 정확히 한 번 방문
+ * `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
+ * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
+ * `A` [Combination Sum](src/algorithms/sets/combination-sum) - 특정 합계를 구성하는 모든 조합 찾기
+
+* **지점 및 바운드** - 역추적 검색의 각 단계에서 발견 된 최저 비용 솔루션을 기억하고 문제에 대한 최소 비용 솔루션의 비용에 대한 최저 한도 인 발견 된 최저 비용 솔루션의 비용을 사용하여 부분적 지금까지 발견 된 최저 비용 솔루션보다 큰 비용의 솔루션. 일반적으로 상태 공간 트리의 DFS 순회와 함께 BFS 순회가 사용됩니다.
+
+## 이 저장소를 사용하는 방법
+
+**의존모듈 설치**
+```
+npm install
+```
+
+**전체 테스트**
+```
+npm test
+```
+
+**이름 별 테스트**
+```
+npm test -- -t 'LinkedList'
+```
+
+**Playground**
+
+`./src/playground/playground.js` 파일에 데이터 구조와 알고리즘을 작성해볼 수 있고, `./src/playground/__test__/playground.test.js`에 테스트를 작성할 수 있습니다.
+
+그런 Playground 코드가 예상대로 작동하는지 테스트하려면 다음 명령을 실행하기 만하면됩니다.
+
+```
+npm test -- -t 'playground'
+```
+
+## 유용한 정보
+
+### 레퍼런스
+
+[▶ Data Structures and Algorithms on YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+
+### 빅 오 표기법(Big O Notation)
+
+Big O 표기법에 지정된 알고리즘의 성장 순서.
+
+
+
+Source: [Big O Cheat Sheet](http://bigocheatsheet.com/).
+
+다음은 가장 많이 사용되는 Big O 표기법과 다양한 크기의 입력 데이터에 대한 성능 비교 목록입니다.
+
+| Big O Notation | Computations for 10 elements | Computations for 100 elements | Computations for 1000 elements |
+| -------------- | ---------------------------- | ----------------------------- | ------------------------------- |
+| **O(1)** | 1 | 1 | 1 |
+| **O(log N)** | 3 | 6 | 9 |
+| **O(N)** | 10 | 100 | 1000 |
+| **O(N log N)** | 30 | 600 | 9000 |
+| **O(N^2)** | 100 | 10000 | 1000000 |
+| **O(2^N)** | 1024 | 1.26e+29 | 1.07e+301 |
+| **O(N!)** | 3628800 | 9.3e+157 | 4.02e+2567 |
+
+### 자료 구조 연산 복잡성
+
+| Data Structure | Access | Search | Insertion | Deletion | Comments |
+| ----------------------- | :-------: | :-------: | :-------: | :-------: | :-------- |
+| **Array** | 1 | n | n | n | |
+| **Stack** | n | n | 1 | 1 | |
+| **Queue** | n | n | 1 | 1 | |
+| **Linked List** | n | n | 1 | 1 | |
+| **Hash Table** | - | n | n | n | 완벽한 해시 함수의 경우 비용은 O (1) |
+| **Binary Search Tree** | n | n | n | n | 균형 잡힌 트리의 경우 비용은 O (log (n)) 이 될 것임. |
+| **B-Tree** | log(n) | log(n) | log(n) | log(n) | |
+| **Red-Black Tree** | log(n) | log(n) | log(n) | log(n) | |
+| **AVL Tree** | log(n) | log(n) | log(n) | log(n) | |
+| **Bloom Filter** | - | 1 | 1 | - | 검색하는 동안 거짓 긍정이 가능합니다. |
+
+### 배열 정렬 알고리즘 복잡성
+
+| Name | Best | Average | Worst | Memory | Stable | Comments |
+| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
+| **Bubble sort** | n | n<sup>2</sup> | n<sup>2</sup> | 1 | Yes | |
+| **Insertion sort** | n | n<sup>2</sup> | n<sup>2</sup> | 1 | Yes | |
+| **Selection sort** | n<sup>2</sup> | n<sup>2</sup> | n<sup>2</sup> | 1 | No | |
+| **Heap sort** | n log(n) | n log(n) | n log(n) | 1 | No | |
+| **Merge sort** | n log(n) | n log(n) | n log(n) | n | Yes | |
+| **Quick sort** | n log(n) | n log(n) | n<sup>2</sup> | log(n) | No | |
+| **Shell sort** | n log(n) | depends on gap sequence | n (log(n))<sup>2</sup> | 1 | No | |
+| **Counting sort** | n + r | n + r | n + r | n + r | Yes | r - biggest number in array |
+| **Radix sort** | n * k | n * k | n * k | n + k | Yes | k - length of longest key |
diff --git a/src/data-structures/doubly-linked-list/README.ko-KR.md b/src/data-structures/doubly-linked-list/README.ko-KR.md
new file mode 100644
index 0000000000..40f2ae58f7
--- /dev/null
+++ b/src/data-structures/doubly-linked-list/README.ko-KR.md
@@ -0,0 +1,12 @@
+# Doubly Linked List
+
+컴퓨터 과학에서 **이중 연결 리스트(Doubly Linked List)**는 노드라고하는 순차적으로 링크 된 레코드 집합으로 구성된 연결된 데이터 구조입니다. 각 노드에는 링크라고하는 두 개의 필드가 있으며 노드 시퀀스에서 이전 노드와 다음 노드에 대한 참조입니다. 시작과 끝 노드는 이전 링크와 다음 링크를 가지며, 각각 목록의 순회를 용이하게하기 위해 일종의 종단점 (일반적으로 감시 노드 또는 null)을 가리 킵니다. 센티넬 노드가 하나만있는 경우 목록은 센티넬 노드를 통해 순환 링크됩니다. 동일한 데이터 항목으로 형성되지만 반대 순차 순서로 형성된 두 개의 단일 연결 목록으로 개념화 될 수 있습니다.
+
+
+
+두 노드 링크는 목록의 탐색을 양방향으로 허용합니다. 이중 링크 목록에서 노드를 추가하거나 제거하려면 단일 링크 목록에서 동일 연산보다 많은 링크를 변경해야하는 반면, 순회 중 이전 노드를 추적하거나 이전 노드를 찾기 위해 목록을 탐색할 필요가 없기 때문에 해당 링크를 수정할 수 있어서 작업이 더 간단하고 잠재적으로 더 효율적입니다(첫 번째 노드가 아닌 노드의 경우).
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Doubly_linked_list)
+- [YouTube](https://www.youtube.com/watch?v=JdQeNxWCguQ&t=7s&index=72&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
diff --git a/src/data-structures/linked-list/README.ko-KR.md b/src/data-structures/linked-list/README.ko-KR.md
new file mode 100644
index 0000000000..72f044a19a
--- /dev/null
+++ b/src/data-structures/linked-list/README.ko-KR.md
@@ -0,0 +1,10 @@
+# Linked List
+
+컴퓨터 과학에서 연결 리스트(Linked List)은 데이터 요소의 선형 집합이며 선형 순서는 메모리의 물리적 배치에 의해 주어지지 않습니다. 대신 각 요소는 다음 요소를 가리 킵니다. 대신 각 요소는 다음 요소를 가리 킵니다. 시퀀스를 함께 나타내는 노드 그룹으로 구성된 데이터 구조입니다. 가장 단순한 형태에서 각 노드는 데이터와 시퀀스의 다음 노드에 대한 참조 (즉, 링크)로 구성됩니다. 이 구조는 반복하는 동안 시퀀스의 임의 위치에서 요소를 효율적으로 삽입하거나 제거 할 수 있습니다. 더 복잡한 변형은 링크를 추가하여 임의의 요소 참조에서 효율적으로 삽입하거나 제거 할 수 있습니다. 연결 목록의 단점은 액세스 시간이 선형 (파이프 라인이 어렵다)이라는 것입니다. 랜덤 액세스와 같은 더 빠른 액세스는 실현 가능하지 않습니다. 배열은 링크 된 목록과 비교하여 캐시 위치가 더 좋습니다.
+
+
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Linked_list)
+- [YouTube](https://www.youtube.com/watch?v=njTh_OwMljA&index=2&t=1s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
diff --git a/src/data-structures/queue/README.ko-KR.md b/src/data-structures/queue/README.ko-KR.md
new file mode 100644
index 0000000000..2f441eb097
--- /dev/null
+++ b/src/data-structures/queue/README.ko-KR.md
@@ -0,0 +1,12 @@
+# Queue
+
+컴퓨터 과학에서, 큐는 추상 데이터 형식 혹은 컬렉션입니다. 컬렉션 내의 엔티티는 순서를 유지하고 컬렉션 상의 기본(혹은 유일한) 연산들이 있습니다. 연산들 중에는 가장 끝단에 엔티티를 추가하는 `enqueue`와 제일 첫번째 엔티티를 제거하는 `dequeue`가 있습니다. 그러면 큐가 FIFO (First In First Out) 데이터 구조가됩니다. FIFO 데이터 구조에서 대기열에 추가 된 첫 번째 요소는 제거 될 첫 번째 요소가됩니다. 이는 새로운 요소가 추가되면 이전에 추가 된 모든 요소를 제거해야 새로운 요소를 제거 할 수 있다는 요구 사항과 동일합니다.프론트 요소의 값을 반환하지 않고 반환하는 엿보기 또는 앞쪽 작업도 종종 입력됩니다. 큐는 선형 데이터 구조의 예이거나 보다 추상적으로 순차적 수집입니다.
+
+FIFO (선입 선출) 대기열 표현
+
+
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Queue_(abstract_data_type))
+- [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&)
From 9d95f0a6611f830353e198bd5afde66ca0bb87fc Mon Sep 17 00:00:00 2001
From: Jeremy Kang <jeremy.kang@obigo.com>
Date: Mon, 9 Jul 2018 18:20:49 +0900
Subject: [PATCH 2/2] =?UTF-8?q?=EC=B6=94=EA=B0=80=20=EC=9E=91=EC=97=85=20?=
=?UTF-8?q?=EC=A7=84=ED=96=89?=
MIME-Version: 1.0
Content-Type: text/plain; charset=UTF-8
Content-Transfer-Encoding: 8bit
---
README.ko-KR.md | 2 +-
src/algorithms/math/bits/README.ko-KR.md | 79 +++++++++++++
.../math/euclidean-algorithm/README.ko-KR.md | 25 +++++
src/algorithms/math/factorial/README.ko-KR.md | 30 +++++
src/algorithms/math/fibonacci/README.ko-KR.md | 17 +++
.../math/integer-partition/README.ko-KR.md | 28 +++++
.../math/is-power-of-two/README.ko-KR.md | 44 ++++++++
.../least-common-multiple/README.ko-KR.md | 48 ++++++++
src/algorithms/math/liu-hui/README.ko-KR.md | 82 ++++++++++++++
.../math/primality-test/README.ko-KR.md | 12 ++
.../sieve-of-eratosthenes/README.ko-KR.md | 29 +++++
.../sets/cartesian-product/README.ko-KR.md | 11 ++
.../sets/combination-sum/README.ko-KR.md | 55 +++++++++
.../sets/combinations/README.ko-KR.md | 70 ++++++++++++
.../sets/fisher-yates/README.ko-KR.md | 7 ++
.../sets/knapsack-problem/README.ko-KR.md | 48 ++++++++
.../README.ko-KR.md | 17 +++
.../README.ko-KR.md | 38 +++++++
.../sets/maximum-subarray/README.ko-KR.md | 17 +++
.../sets/permutations/README.ko-KR.md | 55 +++++++++
src/algorithms/sets/power-set/README.ko-KR.md | 12 ++
.../README.ko-KR.md | 21 ++++
.../levenshtein-distance/README.ko-KR.md | 106 ++++++++++++++++++
23 files changed, 852 insertions(+), 1 deletion(-)
create mode 100644 src/algorithms/math/bits/README.ko-KR.md
create mode 100644 src/algorithms/math/euclidean-algorithm/README.ko-KR.md
create mode 100644 src/algorithms/math/factorial/README.ko-KR.md
create mode 100644 src/algorithms/math/fibonacci/README.ko-KR.md
create mode 100644 src/algorithms/math/integer-partition/README.ko-KR.md
create mode 100644 src/algorithms/math/is-power-of-two/README.ko-KR.md
create mode 100644 src/algorithms/math/least-common-multiple/README.ko-KR.md
create mode 100644 src/algorithms/math/liu-hui/README.ko-KR.md
create mode 100644 src/algorithms/math/primality-test/README.ko-KR.md
create mode 100644 src/algorithms/math/sieve-of-eratosthenes/README.ko-KR.md
create mode 100644 src/algorithms/sets/cartesian-product/README.ko-KR.md
create mode 100644 src/algorithms/sets/combination-sum/README.ko-KR.md
create mode 100644 src/algorithms/sets/combinations/README.ko-KR.md
create mode 100644 src/algorithms/sets/fisher-yates/README.ko-KR.md
create mode 100644 src/algorithms/sets/knapsack-problem/README.ko-KR.md
create mode 100644 src/algorithms/sets/longest-common-subsequence/README.ko-KR.md
create mode 100644 src/algorithms/sets/longest-increasing-subsequence/README.ko-KR.md
create mode 100644 src/algorithms/sets/maximum-subarray/README.ko-KR.md
create mode 100644 src/algorithms/sets/permutations/README.ko-KR.md
create mode 100644 src/algorithms/sets/power-set/README.ko-KR.md
create mode 100644 src/algorithms/sets/shortest-common-supersequence/README.ko-KR.md
create mode 100644 src/algorithms/string/levenshtein-distance/README.ko-KR.md
diff --git a/README.ko-KR.md b/README.ko-KR.md
index b0aa12ce07..1974547f39 100644
--- a/README.ko-KR.md
+++ b/README.ko-KR.md
@@ -50,7 +50,7 @@ _다른 언어로 보실 수 있습니다:_
* `B` [Fibonacci Number](src/algorithms/math/fibonacci)
* `B` [Primality Test](src/algorithms/math/primality-test) (시험 분할 방법)
* `B` [Euclidean Algorithm](src/algorithms/math/euclidean-algorithm) - 최대 공약수(GCD) 계산
- * `B` [Least Common Multiple](src/algorithms/math/least-common-multiple) (LCM)
+ * `B` [Least Common Multiple](src/algorithms/math/least-common-multiple) - 최소 공배수(LCM) 계산
* `A` [Integer Partition](src/algorithms/math/integer-partition)
* `B` [Sieve of Eratosthenes](src/algorithms/math/sieve-of-eratosthenes) - 주어진 한도까지 모든 소수를 찾는 것
* `B` [Is Power of Two](src/algorithms/math/is-power-of-two) - 수치가 2의 거듭 제곱인지 (순진 및 비트 알고리즘)
diff --git a/src/algorithms/math/bits/README.ko-KR.md b/src/algorithms/math/bits/README.ko-KR.md
new file mode 100644
index 0000000000..e6ae505da7
--- /dev/null
+++ b/src/algorithms/math/bits/README.ko-KR.md
@@ -0,0 +1,79 @@
+# Bit Manipulation
+
+#### 비트 가져 오기
+
+이 메서드는 해당 비트를 0 번째 위치로 이동합니다. 그런 다음 '0001`과 같은 비트 패턴을 가진 AND 연산을 수행합니다. 해당 번호를 제외한 원래 번호의 모든 비트가 지워집니다. 관련 비트가 1이면 결과는 '1'이고, 그렇지 않으면 결과는 '0'입니다.
+
+> 자세한 것은`getBit` 함수를 참고하십시오.
+
+#### 비트 설정
+
+이 방법은`bitPosition` 비트에 의해`1`을 시프트하여`00100`과 같은 값을 생성합니다. 그런 다음 특정 비트를 '1'로 설정하는 'OR'연산을 수행하지만 숫자의 다른 비트에는 영향을 미치지 않습니다.
+
+> 자세한 것은`setBit` 함수를 참고하십시오.
+
+#### 비트 지우기
+
+이 방법은`bitPosition` 비트에 의해`1`을 시프트하여`00100`과 같은 값을 생성합니다. 그런 다음 이 마스크를 반전하여 '11011'과 같은 숫자를 얻습니다. 그런 다음 AND와 연산이 숫자와 마스크에 모두 적용됩니다. 이 작업은 비트를 설정 해제합니다.
+
+> 자세한 것은`clearBit` 함수를 참고하십시오.
+
+#### 비트 갱신
+
+이 방법은 "비트 지우기"및 "비트 설정"방법의 조합입니다.
+
+> 자세한 것은`updateBit` 함수를 참고하십시오.
+
+#### 2로 곱하기
+
+이 방법은 원래 숫자를 1 비트 왼쪽으로 이동합니다. 따라서 모든 이진수 구성 요소 (2의 제곱)에 2가 곱해 지므로 숫자 자체에 2가 곱 해집니다.
+
+```
+Before the shift
+Number: 0b0101 = 5
+Powers of two: 0 + 2^2 + 0 + 2^0
+
+After the shift
+Number: 0b1010 = 10
+Powers of two: 2^3 + 0 + 2^1 + 0
+```
+
+> 자세한 것은`multiplyByTwo` 함수를 참고하십시오.
+
+#### 2로 나누기
+
+이 방법은 원래 숫자를 오른쪽으로 1 비트 씩 이동합니다. 따라서 모든 2 진수 구성 요소 (2의 제곱)는 2로 나누어지고 따라서 숫자 자체는 나머지없이 2로 나눕니다.
+
+```
+Before the shift
+Number: 0b0101 = 5
+Powers of two: 0 + 2^2 + 0 + 2^0
+
+After the shift
+Number: 0b0010 = 2
+Powers of two: 0 + 0 + 2^1 + 0
+```
+
+> 자세한 내용은`divideByTwo` 함수를 참고하십시오.
+
+#### 부호 변경
+
+이 메서드는 양수가 음수가 되도록합니다. 이렇게 하려면 "Two's Complement" 접근법을 사용합니다. 이 방법은 숫자의 모든 비트를 반전시키고 1을 더하는 방식으로 수행합니다.
+
+```
+1101 -3
+1110 -2
+1111 -1
+0000 0
+0001 1
+0010 2
+0011 3
+```
+
+> 자세한 내용은`switchSign` 함수를 참고하십시오.
+
+## 레퍼런스
+
+- [Bit Manipulation on YouTube](https://www.youtube.com/watch?v=NLKQEOgBAnw&t=0s&index=28&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [Negative Numbers in binary on YouTube](https://www.youtube.com/watch?v=4qH4unVtJkE&t=0s&index=30&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [Bit Hacks on stanford.edu](https://graphics.stanford.edu/~seander/bithacks.html)
diff --git a/src/algorithms/math/euclidean-algorithm/README.ko-KR.md b/src/algorithms/math/euclidean-algorithm/README.ko-KR.md
new file mode 100644
index 0000000000..4211621675
--- /dev/null
+++ b/src/algorithms/math/euclidean-algorithm/README.ko-KR.md
@@ -0,0 +1,25 @@
+# 유클리드 알고리즘
+
+수학에서 유클리드 알고리즘은 최대 공약수(GCD)를 계산하는 데 효율적인 방법입니다. 최대공약수는 두 숫자의 나머지를 남기지 않고 두 숫자를 나누는 가장 큰 숫자입니다.
+
+유클리드 알고리즘은 더 큰 숫자가 더 작은 숫자와의 차이로 대체되면 두 숫자의 최대 공약수가 변하지 않는다는 원칙에 기반합니다. 예를 들어 `252`와 `105`의 최대공약수는 `21`(`252 = 21 × 12` 와 `105 = 21 × 5`) 이고, `105`와 `252 - 105 = 147`의 최대공약수 역시 `21`입니다. 이 대체가 두 숫자 중 큰 숫자를 줄이기 때문에이 과정을 반복하면 두 숫자가 동일해질 때까지 작은 숫자 쌍이 연속적으로 제공됩니다. 그 때, 그들은 원래의 두 숫자의 GCD입니다.
+
+단계들을 반대로함으로써, 최대공약수는 양수 또는 음의 정수, 예를 들어, `21 = 5 × 105 + (-2) × 252`을 곱한 2 개의 원래 수의 합으로 표현 될 수 있습니다. 이러한 방식으로 최대공약수를 항상 표현할 수 있다는 사실을 Bézout의 정체성이라고합니다.
+
+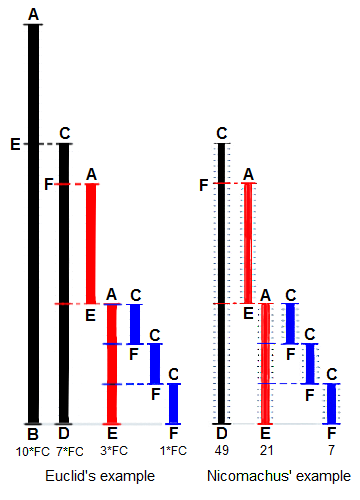
+
+유클리드는 두 개의 시작 길이 인 `BA`와 `DC`의 최대 공약수 (GCD)를 찾는 방법으로 둘 다 공통 "단위"길이의 배수로 정의됩니다. `DC`는 길이가 더 짧고 `BA`를 채우는 데 사용되지만, 남은 `EA`가 `DC`미만이므로 한 번만 사용됩니다. 이제 EA는 더 짧은 길이의 `DC`를 (두 번) 채우고, 남은 `FC`는 `EA`보다 짧습니다. 그러면 `FC`는 `EA`를 (3 번) 채웁니다. 나머지가 없으므로 프로세스는 `FC`가 `GCD`인 것으로 끝납니다. 오른쪽에 Nicomachus의 '49'와 '21'의 예제는 최대공약수는 7이 나온다. (히스 1908 : 300에서 파생 됨)
+
+
+
+`24 x 60`사각형은 10개의 `12 x 12`정사각형 타일로 덮여 있으며, `12`는 `24`와 `60`의 GCD입니다. 보다 일반적으로, `a-by-b`사각형은 `c`가 `a`와 `b`의 공통 제수 일 경우에만 길이가 `c`인 정사각형 타일로 덮을 수 있습니다.
+
+
+
+유클리드 알고리즘의 뺄셈 기반 애니메이션.
+초기 직사각형의 크기는 `a = 1071`과 `b = 462`입니다. `462 × 462` 크기의 사각형이 그 안에 배치되어 `462 × 147` 사각형이 남습니다. 이 직사각형은 `21 × 147`사각형이 남을 때까지 `147 × 147`정사각형으로 바둑판 식으로 배열되며, `21 × 21`정사각형으로 바둑판 식으로 배열되며 덮여지지 않는 영역은 남지 않습니다.
+가장 작은 정사각형 크기 인 `21`은 `1071`과 `462`의 GCD입니다.
+
+## 레퍼런스
+
+[Wikipedia](https://en.wikipedia.org/wiki/Euclidean_algorithm)
diff --git a/src/algorithms/math/factorial/README.ko-KR.md b/src/algorithms/math/factorial/README.ko-KR.md
new file mode 100644
index 0000000000..8a7dd99554
--- /dev/null
+++ b/src/algorithms/math/factorial/README.ko-KR.md
@@ -0,0 +1,30 @@
+# Factorial
+
+수학에서 'n!'으로 표시된 음수가 아닌 정수 'n'의 계승 값은 'n'보다 작거나 같은 모든 양의 정수의 곱입니다. 예를 들면:
+
+```
+5! = 5 * 4 * 3 * 2 * 1 = 120
+```
+
+| n | n! |
+| ----- | --------------------------: |
+| 0 | 1 |
+| 1 | 1 |
+| 2 | 2 |
+| 3 | 6 |
+| 4 | 24 |
+| 5 | 120 |
+| 6 | 720 |
+| 7 | 5 040 |
+| 8 | 40 320 |
+| 9 | 362 880 |
+| 10 | 3 628 800 |
+| 11 | 39 916 800 |
+| 12 | 479 001 600 |
+| 13 | 6 227 020 800 |
+| 14 | 87 178 291 200 |
+| 15 | 1 307 674 368 000 |
+
+## 레퍼런스
+
+[Wikipedia](https://en.wikipedia.org/wiki/Factorial)
diff --git a/src/algorithms/math/fibonacci/README.ko-KR.md b/src/algorithms/math/fibonacci/README.ko-KR.md
new file mode 100644
index 0000000000..5b4e306738
--- /dev/null
+++ b/src/algorithms/math/fibonacci/README.ko-KR.md
@@ -0,0 +1,17 @@
+# Fibonacci Number
+
+수학에서 피보나치 수는 피보나치 수열이라 불리는 다음 정수 계열의 수이고 처음 두 개 이후의 모든 수는 앞의 두 수의 합계입니다:
+
+`0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...`
+
+한 변의 길이가 연속되는 사각형을 가진 기와 피보나치 수
+
+
+
+피보나치 나선형 (Fibonacci spiral) : 피보나치 타일링에서 정사각형의 대각선을 연결하는 원형 호를 그리면서 생성 된 황금 나선의 근사값;[4] 이 크기는 1, 1, 2, 3, 5, 8, 13 및 21 크기의 사각형을 사용합니다.
+
+
+
+## 레퍼런스
+
+[Wikipedia](https://en.wikipedia.org/wiki/Fibonacci_number)
diff --git a/src/algorithms/math/integer-partition/README.ko-KR.md b/src/algorithms/math/integer-partition/README.ko-KR.md
new file mode 100644
index 0000000000..d7164f0766
--- /dev/null
+++ b/src/algorithms/math/integer-partition/README.ko-KR.md
@@ -0,0 +1,28 @@
+# 정수 파티션
+
+수론과 결합론에서 양의 정수 `n` (**정수 파티션**이라고도 함)의 파티션은 양의 정수의 합으로 `n`을 쓰는 방법입니다.
+
+그들의 summand의 순서에서만 다른 2 개의 합계는 동일한 파티션으로 간주됩니다.
+예를 들어, `4`는 다섯 가지 방식으로 분할 될 수 있습니다:
+
+```
+4
+3 + 1
+2 + 2
+2 + 1 + 1
+1 + 1 + 1 + 1
+```
+
+순서에 의존하는 합 `1 + 3`은 `3 + 1`과 같은 파티션이고, `1 + 2 + 1`과 `1 + 1 + 2`는 동일한 파티션 `2 + 1 + 1`으로 표현됩니다.
+
+Young diagrams associated to the partitions of the positive
+integers `1` through `8`. They are arranged so that images
+under the reflection about the main diagonal of the square
+are conjugate partitions.
+
+
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Partition_(number_theory))
+- [YouTube](https://www.youtube.com/watch?v=ZaVM057DuzE&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
diff --git a/src/algorithms/math/is-power-of-two/README.ko-KR.md b/src/algorithms/math/is-power-of-two/README.ko-KR.md
new file mode 100644
index 0000000000..0436251052
--- /dev/null
+++ b/src/algorithms/math/is-power-of-two/README.ko-KR.md
@@ -0,0 +1,44 @@
+# 2의 거듭 제곱 판별
+
+주어진 양의 정수가 2의 거듭 제곱인지 알아내는 함수를 작성하십시오.
+
+**순수 해법**
+
+순수 해법에서는 숫자가 `1`이되지 않는 한 `2`로 나누고, 그 때마다 나머지가 항상 `0`인 것을 확인합니다. 그렇지 않으면 숫자는 `2`의 거듭 제곱이 될 수 없습니다.
+
+**비트단위 해법**
+
+이진 형식의 2의 제곱은 항상 단 하나의 비트를가집니다. 유일한 예외는 부호있는 정수 (예 : `-128`의 값을 갖는 `8`비트 부호있는 정수는 `10000000`과 같습니다.)입니다.
+
+```
+1: 0001
+2: 0010
+4: 0100
+8: 1000
+```
+
+따라서 숫자가 `0`보다 큰지 확인한 후 비트 해킹을 사용하여 하나의 비트 만 설정되어 있는지 테스트 할 수 있습니다.
+
+```
+number & (number - 1)
+```
+
+예를 들어 번호가 `8`이면 다음과 같이 보입니다.:
+
+```
+ 1000
+- 0001
+ ----
+ 0111
+
+ 1000
+& 0111
+ ----
+ 0000
+```
+
+## 예제
+
+- [GeeksForGeeks](https://www.geeksforgeeks.org/program-to-find-whether-a-no-is-power-of-two/)
+- [Bitwise Solution on Stanford](http://www.graphics.stanford.edu/~seander/bithacks.html#DetermineIfPowerOf2)
+- [Binary number subtraction on YouTube](https://www.youtube.com/watch?v=S9LJknZTyos&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=66)
diff --git a/src/algorithms/math/least-common-multiple/README.ko-KR.md b/src/algorithms/math/least-common-multiple/README.ko-KR.md
new file mode 100644
index 0000000000..9169887def
--- /dev/null
+++ b/src/algorithms/math/least-common-multiple/README.ko-KR.md
@@ -0,0 +1,48 @@
+# 최소 공배수
+
+산술과 수론에서, 일반적으로 `LCM (a, b)`로 표시되는 두 정수 `a`와 `b`의 최소 공배수는 `a`와 `b` 둘 다 나눌 수 있는 가장 작은 양의 정수입니다. 0으로 나누어지는 정수가 정의되지 않기 때문에, 이 정의는 `a`와 `b`가 모두 0과 다른 경우에만 의미가 있습니다. 그러나 일부 저작자는`lcm (a, 0)`을 모든`a`에 대해`0`으로 정의합니다. 이는`lcm`을 나눗셈의 격자에서 가장 작은 상한으로 가져간 결과입니다.
+
+## 예제
+
+`4`와 `6`의 최소공배수(LCM)은 무엇인가?
+
+`4`의 배수는 다음과 같다:
+
+```
+4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, ...
+```
+
+그리고 `6`의 배수는 다음과 같다.
+
+```
+6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...
+```
+
+'4'와 '6'의 공통 배수는 단순히 두 목록에있는 숫자입니다:
+
+```
+12, 24, 36, 48, 60, 72, ....
+```
+
+그래서, `4`와 `6`의 처음 몇 개의 공통 배수 목록에서, 최소 공배수는 `12`입니다.
+
+## 최소 공배수 계산
+
+The following formula reduces the problem of computing the least common multiple to the problem of computing the greatest common divisor (GCD), also known as the greatest common factor:
+
+```
+lcm(a, b) = |a * b| / gcd(a, b)
+```
+
+
+
+A Venn diagram showing the least common multiples of combinations of `2`, `3`, `4`, `5` and `7` (`6` is skipped as it is `2 × 3`, both of which are already represented).
+
+For example, a card game which requires its cards to be
+divided equally among up to `5` players requires at least `60`
+cards, the number at the intersection of the `2`, `3`, `4`
+and `5` sets, but not the `7` set.
+
+## References
+
+[Wikipedia](https://en.wikipedia.org/wiki/Least_common_multiple)
diff --git a/src/algorithms/math/liu-hui/README.ko-KR.md b/src/algorithms/math/liu-hui/README.ko-KR.md
new file mode 100644
index 0000000000..f5f39082ef
--- /dev/null
+++ b/src/algorithms/math/liu-hui/README.ko-KR.md
@@ -0,0 +1,82 @@
+# 루후이 π 알고리즘
+
+Liu Hui remarked in his commentary to The Nine Chapters on the Mathematical Art, that the ratio of the circumference of an inscribed hexagon to the diameter of the circle was `three`, hence `π` must be greater than three. He went on to provide a detailed step-by-step description of an iterative algorithm to calculate `π` to any required accuracy based on bisecting polygons; he calculated `π` to between `3.141024` and `3.142708` with a 96-gon; he suggested that `3.14` was a good enough approximation, and expressed `π` as `157/50`; he admitted that this number was a bit small. Later he invented an ingenious quick method to improve on it, and obtained `π ≈ 3.1416` with only a 96-gon, with an accuracy comparable to that from a 1536-gon. His most important contribution in this area was his simple iterative `π` algorithm.
+
+## Area of a circle
+
+Liu Hui argued:
+
+> Multiply one side of a hexagon by the radius (of its
+circumcircle), then multiply this by three, to yield the
+area of a dodecagon; if we cut a hexagon into a
+dodecagon, multiply its side by its radius, then again
+multiply by six, we get the area of a 24-gon; the finer
+we cut, the smaller the loss with respect to the area
+of circle, thus with further cut after cut, the area of
+the resulting polygon will coincide and become one with
+the circle; there will be no loss
+
+
+
+Liu Hui's method of calculating the area of a circle.
+
+Further, Liu Hui proved that the area of a circle is half of its circumference
+multiplied by its radius. He said:
+
+> Between a polygon and a circle, there is excess radius. Multiply the excess
+radius by a side of the polygon. The resulting area exceeds the boundary of
+the circle
+
+In the diagram `d = excess radius`. Multiplying `d` by one side results in
+oblong `ABCD` which exceeds the boundary of the circle. If a side of the polygon
+is small (i.e. there is a very large number of sides), then the excess radius
+will be small, hence excess area will be small.
+
+> Multiply the side of a polygon by its radius, and the area doubles;
+hence multiply half the circumference by the radius to yield the area of circle.
+
+
+
+The area within a circle is equal to the radius multiplied by half the
+circumference, or `A = r x C/2 = r x r x π`.
+
+## Iterative algorithm
+
+Liu Hui began with an inscribed hexagon. Let `M` be the length of one side `AB` of
+hexagon, `r` is the radius of circle.
+
+
+
+Bisect `AB` with line `OPC`, `AC` becomes one side of dodecagon (12-gon), let
+its length be `m`. Let the length of `PC` be `j` and the length of `OP` be `G`.
+
+`AOP`, `APC` are two right angle triangles. Liu Hui used
+the [Gou Gu](https://en.wikipedia.org/wiki/Pythagorean_theorem) (Pythagorean theorem)
+theorem repetitively:
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+From here, there is now a technique to determine `m` from `M`, which gives the
+side length for a polygon with twice the number of edges. Starting with a
+hexagon, Liu Hui could determine the side length of a dodecagon using this
+formula. Then continue repetitively to determine the side length of a
+24-gon given the side length of a dodecagon. He could do this recursively as
+many times as necessary. Knowing how to determine the area of these polygons,
+Liu Hui could then approximate `π`.
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Liu_Hui%27s_%CF%80_algorithm)
diff --git a/src/algorithms/math/primality-test/README.ko-KR.md b/src/algorithms/math/primality-test/README.ko-KR.md
new file mode 100644
index 0000000000..3c43170575
--- /dev/null
+++ b/src/algorithms/math/primality-test/README.ko-KR.md
@@ -0,0 +1,12 @@
+# 소수 테스트
+
+** 소수 ** (또는 ** 소수 **)는 두 개의 더 작은 자연수를 곱하여 형성 할 수없는 '1'보다 큰 자연수입니다. '소수'가 아닌 자연수를 합성수라고합니다. 예를 들어 '5'는 소수로, '1 × 5'또는 '5 × 1'이라는 제품으로 쓰는 유일한 방법은 '5'자체를 포함하기 때문입니다. 그러나 '6'은 둘 다 '6'보다 작은 두 개의 숫자 (2 × 3)의 곱이므로 합성수입니다.
+
+
+
+** 소수 테스트 **는 입력 숫자가 소수인지 여부를 결정하는 알고리즘입니다. 다른 수학 분야 중에서도 암호학에 사용됩니다. 인수분해와 달리 소수 테스트는 일반적으로 입력 요소가 소수인지 아닌지만을 나타내는 소수 요소를 제공하지 않습니다. 인수분해는 계산적으로 어려운 문제로 생각되지만 소수 테스트는 비교적 쉽습니다 (실행 시간은 입력 크기에서 다항식입니다).
+
+## 레퍼런스
+
+- [Prime Numbers on Wikipedia](https://en.wikipedia.org/wiki/Prime_number)
+- [Primality Test on Wikipedia](https://en.wikipedia.org/wiki/Primality_test)
diff --git a/src/algorithms/math/sieve-of-eratosthenes/README.ko-KR.md b/src/algorithms/math/sieve-of-eratosthenes/README.ko-KR.md
new file mode 100644
index 0000000000..e55709df85
--- /dev/null
+++ b/src/algorithms/math/sieve-of-eratosthenes/README.ko-KR.md
@@ -0,0 +1,29 @@
+# 에라토스테네스 체
+
+에라토스테네스 체는 어떤 `n`까지 모든 소수를 찾는 알고리즘입니다.
+
+그것은 고대 그리스 수학자 인 키레네(Cyrene)의 에라토스테네스(Eratosthenes)에 기인합니다.
+
+## 동작 원리
+
+1. Create a boolean array of `n + 1` positions (to represent the numbers `0` through `n`)
+2. Set positions `0` and `1` to `false`, and the rest to `true`
+3. Start at position `p = 2` (the first prime number)
+4. Mark as `false` all the multiples of `p` (that is, positions `2 * p`, `3 * p`, `4 * p`... until you reach the end of the array)
+5. Find the first position greater than `p` that is `true` in the array. If there is no such position, stop. Otherwise, let `p` equal this new number (which is the next prime), and repeat from step 4
+
+When the algorithm terminates, the numbers remaining `true` in the array are all the primes below `n`.
+
+An improvement of this algorithm is, in step 4, start marking multiples of `p` from `p * p`, and not from `2 * p`. The reason why this works is because, at that point, smaller multiples of `p` will have already been marked `false`.
+
+## 예제
+
+
+
+## 복잡도
+
+The algorithm has a complexity of `O(n log(log n))`.
+
+## 레퍼런스
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes)
diff --git a/src/algorithms/sets/cartesian-product/README.ko-KR.md b/src/algorithms/sets/cartesian-product/README.ko-KR.md
new file mode 100644
index 0000000000..3c3e1cc003
--- /dev/null
+++ b/src/algorithms/sets/cartesian-product/README.ko-KR.md
@@ -0,0 +1,11 @@
+# 데카르트 곱
+
+집합 이론에서 데카르트 곱은 여러 세트로부터 집합 (또는 집합 또는 단순히 곱)을 반환하는 수학 연산입니다. 즉, 집합 A와 B에 대해, 데카르트 곱 A × B는 a ∈ A와 b ∈ B인 모든 순서쌍 (a, b)의 집합이다.
+
+Cartesian product `AxB` of two sets `A={x,y,z}` and `B={1,2,3}`
+
+
+
+## References
+
+[Wikipedia](https://en.wikipedia.org/wiki/Cartesian_product)
diff --git a/src/algorithms/sets/combination-sum/README.ko-KR.md b/src/algorithms/sets/combination-sum/README.ko-KR.md
new file mode 100644
index 0000000000..8d24eb4430
--- /dev/null
+++ b/src/algorithms/sets/combination-sum/README.ko-KR.md
@@ -0,0 +1,55 @@
+# 조합의 합 문제
+
+후보 번호 (`후보`) **(중복 없음)** 및 대상 번호 (`대상`)의 **집합** 이 주어지면, 후보 번호가 `대상`과 합쳐진 `후보`의 모든 고유 한 조합을 찾습니다 .
+
+**동일한** 반복 번호는 `후보`에서 무제한으로 선택할 수 있습니다.
+
+**참고:**
+
+- 모든 숫자 (`target` 포함)는 양의 정수입니다.
+- 정답 집합에는 중복된 조합이 없어야합니다.
+
+## 예제
+
+```
+Input: candidates = [2,3,6,7], target = 7,
+
+A solution set is:
+[
+ [7],
+ [2,2,3]
+]
+```
+
+```
+Input: candidates = [2,3,5], target = 8,
+
+A solution set is:
+[
+ [2,2,2,2],
+ [2,3,3],
+ [3,5]
+]
+```
+
+## 설명
+
+문제는 최상의 결과 나 결과의 수가 아닌 가능한 모든 결과를 얻는 것이기 때문에, DP (동적 프로그래밍)를 고려할 필요가 없으므로, 이를 처리하기 위해 재귀를 사용하는 역추적 접근이 필요합니다.
+
+다음은`candidate = [2, 3]` 및 `target = 6` 상황에 대한 의사 결정 트리의 예입니다:
+
+```
+ 0
+ / \
+ +2 +3
+ / \ \
+ +2 +3 +3
+ / \ / \ \
+ +2 ✘ ✘ ✘ ✓
+ / \
+ ✓ ✘
+```
+
+## 참고 자료
+
+- [LeetCode](https://leetcode.com/problems/combination-sum/description/)
diff --git a/src/algorithms/sets/combinations/README.ko-KR.md b/src/algorithms/sets/combinations/README.ko-KR.md
new file mode 100644
index 0000000000..3d39cbb1fd
--- /dev/null
+++ b/src/algorithms/sets/combinations/README.ko-KR.md
@@ -0,0 +1,70 @@
+# 조합
+
+순서가 중요하지 않다면, 그것은 **조합**입니다.
+
+순서가 **중요할 때**, 그것은 **순열**입니다.
+
+**"My fruit salad is a combination of apples, grapes and bananas"**
+We don't care what order the fruits are in, they could also be
+"bananas, grapes and apples" or "grapes, apples and bananas",
+its the same fruit salad.
+
+## 반복없는 조합
+
+This is how lotteries work. The numbers are drawn one at a
+time, and if we have the lucky numbers (no matter what order)
+we win!
+
+No Repetition: such as lottery numbers `(2,14,15,27,30,33)`
+
+**Number of combinations**
+
+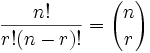
+
+where `n` is the number of things to choose from, and we choose `r` of them,
+no repetition, order doesn't matter.
+
+It is often called "n choose r" (such as "16 choose 3"). And is also known as the Binomial Coefficient.
+
+## 반복 조합
+
+Repetition is Allowed: such as coins in your pocket `(5,5,5,10,10)`
+
+Or let us say there are five flavours of ice cream:
+`banana`, `chocolate`, `lemon`, `strawberry` and `vanilla`.
+
+We can have three scoops. How many variations will there be?
+
+Let's use letters for the flavours: `{b, c, l, s, v}`.
+Example selections include:
+
+- `{c, c, c}` (3 scoops of chocolate)
+- `{b, l, v}` (one each of banana, lemon and vanilla)
+- `{b, v, v}` (one of banana, two of vanilla)
+
+**조합의 갯수**
+
+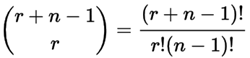
+
+Where `n` is the number of things to choose from, and we
+choose `r` of them. Repetition allowed,
+order doesn't matter.
+
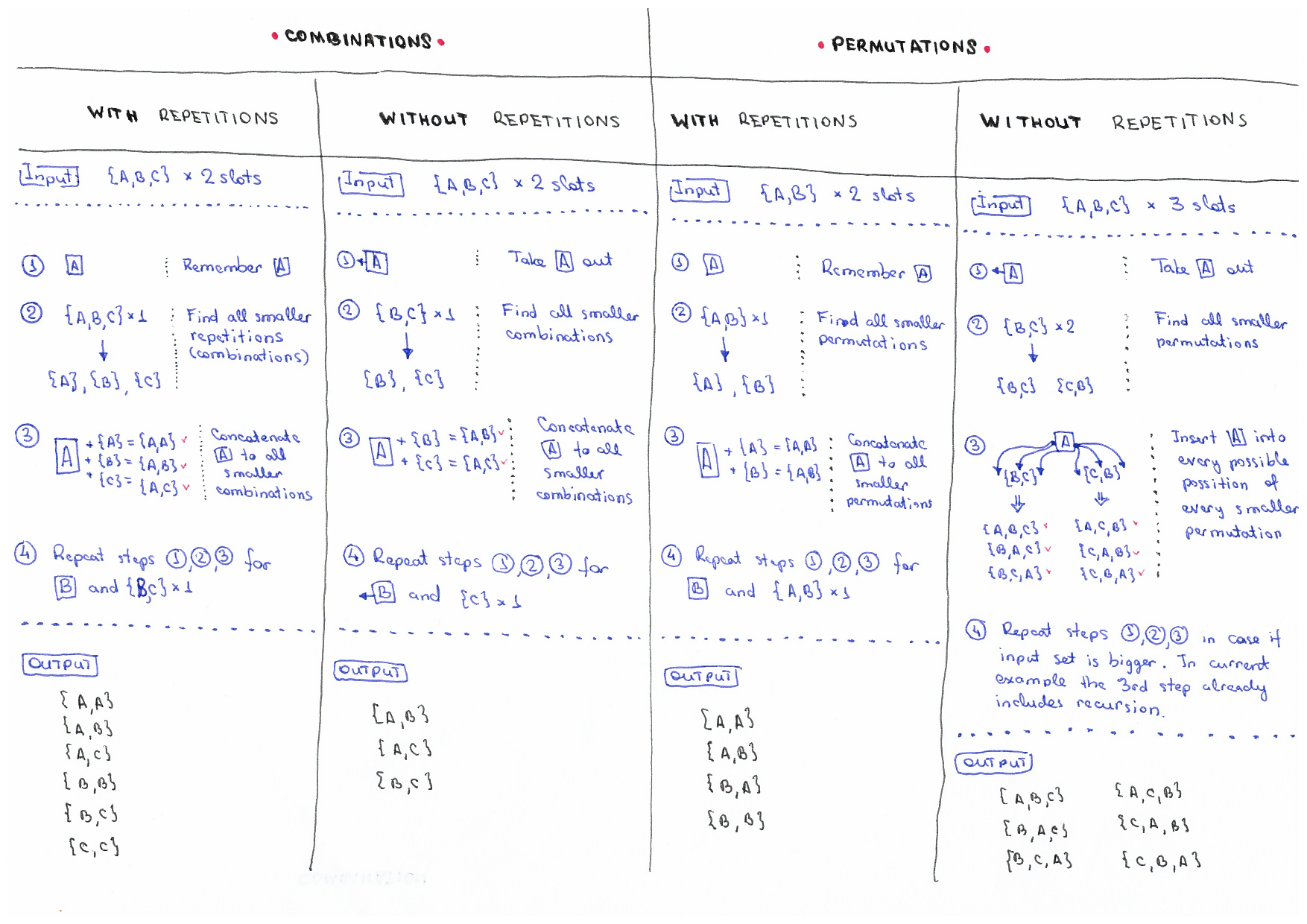
+## Cheat Sheets
+
+Permutations cheat sheet
+
+
+
+Combinations cheat sheet
+
+
+
+Permutations/combinations algorithm ideas.
+
+
+
+## References
+
+- [Math Is Fun](https://www.mathsisfun.com/combinatorics/combinations-permutations.html)
+- [Permutations/combinations cheat sheets](https://medium.com/@trekhleb/permutations-combinations-algorithms-cheat-sheet-68c14879aba5)
diff --git a/src/algorithms/sets/fisher-yates/README.ko-KR.md b/src/algorithms/sets/fisher-yates/README.ko-KR.md
new file mode 100644
index 0000000000..a6498729ef
--- /dev/null
+++ b/src/algorithms/sets/fisher-yates/README.ko-KR.md
@@ -0,0 +1,7 @@
+# 피셔-예이츠 셔플
+
+Fisher-Yates 셔플은 유한 시퀀스의 무작위 순열을 생성하는 알고리즘입니다 - 일반 용어로 알고리즘은 시퀀스를 뒤섞습니다. 알고리즘은 효과적으로 모든 요소를 모자에 넣습니다; 요소가 남아 있지 않을 때까지 요소를 모자에서 무작위로 그린 다음 요소를 계속 결정합니다. 이 알고리즘은 편향 순열을 만듭니다: 모든 순열은 똑같이 비슷합니다. 최신 버전의 알고리즘이 효율적입니다:셔플되는 아이템의 수에 비례하여 시간이 걸리고 그들을 제자리에 셔플합니다.
+
+## References
+
+[Wikipedia](https://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle)
diff --git a/src/algorithms/sets/knapsack-problem/README.ko-KR.md b/src/algorithms/sets/knapsack-problem/README.ko-KR.md
new file mode 100644
index 0000000000..4c5eb176c0
--- /dev/null
+++ b/src/algorithms/sets/knapsack-problem/README.ko-KR.md
@@ -0,0 +1,48 @@
+# 배낭 문제
+
+배낭 문제는 조합 최적화 문제입니다: 각각 무게와 가격이 있는 아이템들의 집합이 주어진다면, 집합에 들어갈 수 있는 각 아이템의 갯수를 정하십시오. 단, 총 무게는 주어진 제한 무게 이하여야 하고, 총 가격은 최대한 커야 합니다.
+
+그것은 고정 크기 배낭에 의해 제약받는 사람이 직면 한 문제에서 그 이름을 파생시키고 그것을 가장 가치있는 항목으로 채워야합니다.
+
+1 차원 (구속) 배낭 문제의 예 : 전체 중량을 15kg 이하로 유지하면서 금액을 최대화하기 위해 어떤 상자를 선택해야합니까?
+
+
+
+## 정의
+
+### 0/1 배낭 문제
+
+풀 수 있는 가장 일반적인 문제는 **0/1 배낭 문제**이며, 각 종류의 항목의 복사본 수를 0또는 1까지 각 아이템의 **x<sub>i</sub>** 수로 제한합니다.
+
+`1`에서 `n`까지 번호가 매겨진 n 개의 항목 집합에서, 각각 무게 **w<sub>i</sub>** 와 가격 **v<sub>i</sub>** 이고, 최대 무게 용량은 `W`이 주어진다면,
+
+maximize 
+
+subject to  and 
+
+이다.
+
+여기서 **x<sub>i</sub>** 는 배낭에 포함시킬 항목 `i`의 인스턴스의 수를 나타냅니다. 비공식적으로, 문제는 무게의 합이 배낭의 용량보다 작거나 같도록 배낭의 항목 값의 합을 최대화하는 것입니다.
+
+### 경계 배낭 문제 (BKP)
+
+**경계 배낭 문제 (BKP)** 는 각 항목 중 하나만 있다는 제한을 없애고 각 항목 종류의 복사본의 수 **x<sub>i</sub>** 를 최대 음이 아닌 정수 값 `c`로 제한합니다:
+
+maximize 
+
+subject to 
+and 
+
+### 무한 배낭 문제 (UKP)
+
+**무한 배낭 문제 (UKP)** 는 각 종류의 항목의 복사본 수에 상한선을 두지 않으며 위와 같이 공식화 될 수 있습니다. 단, **x<sub>i</sub>** 에 대한 유일한 제한은 음수가 아닌 정수입니다.
+
+maximize 
+
+subject to 
+and 
+
+## 레퍼런스
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Knapsack_problem)
+- [0/1 Knapsack Problem on YouTube](https://www.youtube.com/watch?v=8LusJS5-AGo&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
diff --git a/src/algorithms/sets/longest-common-subsequence/README.ko-KR.md b/src/algorithms/sets/longest-common-subsequence/README.ko-KR.md
new file mode 100644
index 0000000000..0da6ef5d15
--- /dev/null
+++ b/src/algorithms/sets/longest-common-subsequence/README.ko-KR.md
@@ -0,0 +1,17 @@
+# 가장 긴 공통 서브 시퀀스 문제
+
+LCS (Longest Common Subsequence) 문제는 일련의 시퀀스 (종종 두 시퀀스 만)에서 모든 시퀀스에 공통된 가장 긴 하위 시퀀스를 찾는 문제입니다. 하위 문자열과 달리 하위 시퀀스는 원래 시퀀스 내에서 연속적인 위치를 차지할 필요가 없습니다.
+
+## 응용 분야
+
+가장 긴 공통 서브 시퀀스 문제는 diff 유틸리티와 같은 데이터 비교 프로그램의 기초가되는 고전적인 컴퓨터 과학 문제이며, 생물 정보학 분야의 응용 프로그램을 가지고 있습니다. 또한 Git과 같은 변경 관리 시스템에서 변경 관리 제어 파일 모음의 여러 변경 사항을 조정할 때 널리 사용됩니다.
+
+## 예제
+
+- LCS for input Sequences `ABCDGH` and `AEDFHR` is `ADH` of length 3.
+- LCS for input Sequences `AGGTAB` and `GXTXAYB` is `GTAB` of length 4.
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Longest_common_subsequence_problem)
+- [YouTube](https://www.youtube.com/watch?v=NnD96abizww&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
diff --git a/src/algorithms/sets/longest-increasing-subsequence/README.ko-KR.md b/src/algorithms/sets/longest-increasing-subsequence/README.ko-KR.md
new file mode 100644
index 0000000000..7a1b4d4746
--- /dev/null
+++ b/src/algorithms/sets/longest-increasing-subsequence/README.ko-KR.md
@@ -0,0 +1,38 @@
+# 가장 길게 증가하는 서브 시퀀스
+
+가장 길게 증가하는 서브 시퀀스 문제는 서브 시퀀스의 요소가 정렬 순서대로, 가장 낮은 순서에서, 그리고 서브 시퀀스가 가능한 한 길게 주어진 시퀀스의 서브 시퀀스를 찾는 것입니다. 이 하위 시퀀스는 반드시 연속적이거나 고유하지 않습니다.
+
+## 복잡도
+
+가장 길게 증가하는 서브 시퀀스 문제는 시간 `O (n log n)`에서 풀 수 있는데, 여기서 `n`은 입력 시퀀스의 길이를 나타냅니다.
+
+동적 프로그래밍 접근법은 복잡도가 `O(n * n)`입니다.
+
+## 예제
+
+이진 Van der Corput 시퀀스의 첫 16 항에서
+
+```
+0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15
+```
+
+가장 길게 증가하는 서브 시퀀스는 다음과 같다.
+
+```
+0, 2, 6, 9, 11, 15.
+```
+
+이 하위 시퀀스의 길이는 6입니다. 입력 시퀀스에는 7 개 멤버 증가 시퀀스가 없습니다. 이 예제에서 가장 길게 증가하는 서브 시퀀스는 고유하지 않습니다: 예를 들면,
+
+```
+0, 4, 6, 9, 11, 15 or
+0, 2, 6, 9, 13, 15 or
+0, 4, 6, 9, 13, 15
+```
+
+는 동일한 입력 순서에서 동일한 길이의 다른 증가하는 서브 시퀀스입니다.
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Longest_increasing_subsequence)
+- [Dynamic Programming Approach on YouTube](https://www.youtube.com/watch?v=CE2b_-XfVDk&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
diff --git a/src/algorithms/sets/maximum-subarray/README.ko-KR.md b/src/algorithms/sets/maximum-subarray/README.ko-KR.md
new file mode 100644
index 0000000000..842a111820
--- /dev/null
+++ b/src/algorithms/sets/maximum-subarray/README.ko-KR.md
@@ -0,0 +1,17 @@
+# 최대 부분 배열 문제
+
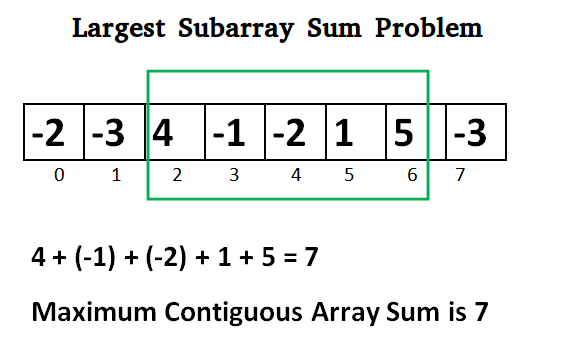
+최대 부분 배열 문제는 가장 큰 합을 갖는 수의 1 차원 배열, 즉 a [1 ... n] 내에서 인접한 부분 배열을 다음과 같이 찾는 작업입니다,
+
+
+
+
+
+## 예제
+
+목록은 일반적으로 '0'과 함께 양수와 음수를 모두 포함합니다. 예를 들어, `-2, 1, -3, 4, -1, 2, 1, -5, 4`의 배열의 경우, 가장 큰 합을 가진 연속적인 부분 배열은 `4, -1, 2`, 합계는 `6`입니다.
+
+## 참고자료
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Maximum_subarray_problem)
+- [YouTube](https://www.youtube.com/watch?v=ohHWQf1HDfU&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [GeeksForGeeks](https://www.geeksforgeeks.org/largest-sum-contiguous-subarray/)
diff --git a/src/algorithms/sets/permutations/README.ko-KR.md b/src/algorithms/sets/permutations/README.ko-KR.md
new file mode 100644
index 0000000000..dc60f2627f
--- /dev/null
+++ b/src/algorithms/sets/permutations/README.ko-KR.md
@@ -0,0 +1,55 @@
+# 순열
+
+순서가 중요하지 않다면, 그것은 **조합**입니다.
+
+순서가 **중요할 때**, 그것은 **순열**입니다.
+
+**"금고 조합은 472입니다"**. 우리는 순서에 유의해야 합니다. `724`는 동작하지 않으며, `247` 또한 마찬가지입니다.
+정확히 `4-7-2`가 되어야 합니다..
+
+## 반복없는 순열
+
+"배열 번호"또는 "순서"라고도하는 순열은 순서가 지정된 목록의 요소를 `S` 자체와 일대일로 다시 구성한 것입니다.
+
+Below are the permutations of string `ABC`.
+
+`ABC ACB BAC BCA CBA CAB`
+
+Or for example the first three people in a running race: you can't be first and second.
+
+**조합의 갯수**
+
+```
+n * (n-1) * (n -2) * ... * 1 = n!
+```
+
+## 반복 순열
+
+반복이 허용될 때, 우리는 반복 순열을 가집니다. 예를 들어 아래 열쇠에서 `333`이 될 수 있습니다.
+
+
+
+**조합의 갯수**
+
+```
+n * n * n ... (r times) = n^r
+```
+
+## Cheat Sheets
+
+Permutations cheat sheet
+
+
+
+Combinations cheat sheet
+
+
+
+Permutations/combinations algorithm ideas.
+
+
+
+## References
+
+- [Math Is Fun](https://www.mathsisfun.com/combinatorics/combinations-permutations.html)
+- [Permutations/combinations cheat sheets](https://medium.com/@trekhleb/permutations-combinations-algorithms-cheat-sheet-68c14879aba5)
diff --git a/src/algorithms/sets/power-set/README.ko-KR.md b/src/algorithms/sets/power-set/README.ko-KR.md
new file mode 100644
index 0000000000..5551ea3550
--- /dev/null
+++ b/src/algorithms/sets/power-set/README.ko-KR.md
@@ -0,0 +1,12 @@
+# Power Set
+
+Power set of a set A is the set of all of the subsets of A.
+
+Eg. for `{x, y, z}`, the subsets are : `{{}, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}, {x, y, z}}`
+
+
+
+## References
+
+* [Wikipedia](https://en.wikipedia.org/wiki/Power_set)
+* [Math is Fun](https://www.mathsisfun.com/sets/power-set.html)
diff --git a/src/algorithms/sets/shortest-common-supersequence/README.ko-KR.md b/src/algorithms/sets/shortest-common-supersequence/README.ko-KR.md
new file mode 100644
index 0000000000..cb0bd8da11
--- /dev/null
+++ b/src/algorithms/sets/shortest-common-supersequence/README.ko-KR.md
@@ -0,0 +1,21 @@
+# 최단 공통 수퍼 시퀀스
+
+두 시퀀스 'X'와 'Y'의 최단 공통 수위 (SCS)는 서브 시퀀스로 'X'와 'Y'를 갖는 최단 시퀀스입니다.
+
+즉, 우리는 두 개의 문자열 str1과 str2가 주어 졌다고 가정하고, str1과 str2를 서브 시퀀스로 갖는 가장 짧은 문자열을 찾습니다.
+
+이것은 가장 긴 공통 서브 시퀀스 문제와 밀접한 관련이있는 문제입니다.
+
+## 예제
+
+```
+Input: str1 = "geek", str2 = "eke"
+Output: "geeke"
+
+Input: str1 = "AGGTAB", str2 = "GXTXAYB"
+Output: "AGXGTXAYB"
+```
+
+## 레퍼런스
+
+- [GeeksForGeeks](https://www.geeksforgeeks.org/shortest-common-supersequence/)
diff --git a/src/algorithms/string/levenshtein-distance/README.ko-KR.md b/src/algorithms/string/levenshtein-distance/README.ko-KR.md
new file mode 100644
index 0000000000..55f286906e
--- /dev/null
+++ b/src/algorithms/string/levenshtein-distance/README.ko-KR.md
@@ -0,0 +1,106 @@
+# Levenshtein 거리
+
+Levenshtein 거리는 두 시퀀스 간의 차이를 측정하기위한 문자열 메트릭입니다. 비공식적으로, 두 단어 사이의 Levenshtein 거리는 한 단어를 다른 단어로 바꾸는 데 필요한 최소 한 문자 편집 (삽입, 삭제 또는 대체) 횟수입니다.
+
+## 정의
+
+수학적으로 두 문자열 사이의 Levenshtein 거리
+`a`와`b` (각각 길이`| a |`와`| b |`)는 다음과 같이 의해 주어진다.
+
+
+
+where
+
+
+
+where
+
+
+
+is the indicator function equal to `0` when
+
+
+
+and equal to 1 otherwise, and
+
+
+
+is the distance between the first `i` characters of `a` and the first `j` characters of `b`.
+
+Note that the first element in the minimum corresponds to deletion (from `a` to `b`), the second to insertion and the third to match or mismatch, depending on whether the respective symbols are the same.
+
+## 예제
+
+For example, the Levenshtein distance between `kitten` and `sitting` is `3`, since the following three edits change one into the other, and there is no way to do it with fewer than three edits:
+
+1. **k**itten → **s**itten (substitution of "s" for "k")
+2. sitt**e**n → sitt**i**n (substitution of "i" for "e")
+3. sittin → sittin**g** (insertion of "g" at the end).
+
+## 응용 분야
+
+여기에는 맞춤법 검사기, 광학 문자 인식 교정 시스템, 퍼지 문자열 검색 및 번역 메모리를 기반으로 자연어 번역을 지원하는 소프트웨어와 같은 다양한 응용 프로그램이 있습니다.
+
+## 동적 프로그래밍 접근법 설명
+
+`ME`와 `MY` 사이의 최소 편집 거리를 찾는 간단한 예제를 살펴 보겠습니다. 직관적으로 당신은 이미 최소 편집 거리가 `1` 연산이고 이 연산을 이미 알고 있습니다. 그리고 그것은`E`를 `Y`로 대체하는 것입니다. 그러나 `Saturday`를 `Sunday`로 변환하는 것과 같은 보다 복잡한 예제를 수행 할 수 있도록 알고리즘의 형식으로 공식화합시다.
+
+To apply the mathematical formula mentioned above to `ME → MY` transformation
+we need to know minimum edit distances of `ME → M`, `M → MY` and `M → M` transformations
+in prior. Then we will need to pick the minimum one and add _one_ operation to
+transform last letters `E → Y`. So minimum edit distance of `ME → MY` transformation
+is being calculated based on three previously possible transformations.
+
+To explain this further let’s draw the following matrix:
+
+
+
+- Cell `(0:1)` contains red number 1. It means that we need 1 operation to
+transform `M` to an empty string. And it is by deleting `M`. This is why this number is red.
+- Cell `(0:2)` contains red number 2. It means that we need 2 operations
+to transform `ME` to an empty string. And it is by deleting `E` and `M`.
+- Cell `(1:0)` contains green number 1. It means that we need 1 operation
+to transform an empty string to `M`. And it is by inserting `M`. This is why this number is green.
+- Cell `(2:0)` contains green number 2. It means that we need 2 operations
+to transform an empty string to `MY`. And it is by inserting `Y` and `M`.
+- Cell `(1:1)` contains number 0. It means that it costs nothing
+to transform `M` into `M`.
+- Cell `(1:2)` contains red number 1. It means that we need 1 operation
+to transform `ME` to `M`. And it is be deleting `E`.
+- And so on...
+
+This looks easy for such small matrix as ours (it is only `3x3`). But here you
+may find basic concepts that may be applied to calculate all those numbers for
+bigger matrices (let’s say `9x7` one, for `Saturday → Sunday` transformation).
+
+According to the formula you only need three adjacent cells `(i-1:j)`, `(i-1:j-1)`, and `(i:j-1)` to
+calculate the number for current cell `(i:j)`. All we need to do is to find the
+minimum of those three cells and then add `1` in case if we have different
+letters in `i`'s row and `j`'s column.
+
+You may clearly see the recursive nature of the problem.
+
+
+
+Let's draw a decision graph for this problem.
+
+
+
+You may see a number of overlapping sub-problems on the picture that are marked
+with red. Also there is no way to reduce the number of operations and make it
+less then a minimum of those three adjacent cells from the formula.
+
+Also you may notice that each cell number in the matrix is being calculated
+based on previous ones. Thus the tabulation technique (filling the cache in
+bottom-up direction) is being applied here.
+
+Applying this principles further we may solve more complicated cases like
+with `Saturday → Sunday` transformation.
+
+
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Levenshtein_distance)
+- [YouTube](https://www.youtube.com/watch?v=We3YDTzNXEk&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [ITNext](https://itnext.io/dynamic-programming-vs-divide-and-conquer-2fea680becbe)