# Árvore Vermelha-Preta (Red-Black Tree) Uma **árvore vermelha-preta** é um tipo de árvore de pesquisa binária auto balanceada na ciência da computação. Cada nó da árvore binária possui um _bit_ extra, e este _bit_ é frequentemente interpretado com a cor (vermelho ou preto) do nó. Estas cores de _bits_ são utilizadas para garantir que a árvore permanece aproximadamente equilibrada durante as operações de inserções e remoções. O equilíbrio é preservado através da pintura de cada nó da árvore com uma das duas cores, de maneira que satisfaça certas propriedades, das quais restringe nos piores dos casos, o quão desequilibrada a árvore pode se tornar. Quando a árvore é modificada, a nova árvore é subsequentemente reorganizada e repintada para restaurar as propriedades de coloração. As propriedades são designadas de tal modo que esta reorganização e nova pintura podem ser realizadas eficientemente. O balanceamento de uma árvore não é perfeito, mas é suficientemente bom para permitir e garantir uma pesquisa no tempo `O(log n)`, aonde `n` é o número total de elementos na árvore. Operações de inserções e remoções, juntamente com a reorganização e repintura da árvore, também são executados no tempo `O (log n)`. Um exemplo de uma árvore vermalha-preta:  ## Propriedades Em adição aos requerimentos impostos pela árvore de pesquisa binária, as seguintes condições devem ser satisfeitas pela árvore vermelha-preta: - Cada nó é tanto vermelho ou preto. - O nó raíz é preto. Esta regra algumas vezes é omitida. Tendo em vista que a raíz pode sempre ser alterada de vermelho para preto, mas não de preto para vermelho, esta regra tem pouco efeito na análise. - Todas as folhas (Nulo/NIL) são pretas. - Caso um nó é vermelho, então seus filhos serão pretos. - Cada caminho de um determinado nó para qualquer um dos seus nós nulos (NIL) descendentes contém o mesmo número de nós pretos. Algumas definições: o número de nós pretos da raiz até um nó é a **profundidade preta**(_black depth_) do nó; o número uniforme de nós pretos em todos os caminhos da raíz até as folhas são chamados de **altura negra** (_black-height_) da árvore vermelha-preta. Essas restrições impõem uma propriedade crítica de árvores vermelhas e pretas: _o caminho da raiz até a folha mais distante não possui mais que o dobro do comprimento do caminho da raiz até a folha mais próxima_. O resultado é que a árvore é grosseiramente balanceada na altura. Tendo em vista que operações como inserções, remoção e pesquisa de valores requerem nos piores dos casos um tempo proporcional a altura da ávore, este limite superior teórico na altura permite que as árvores vermelha-preta sejam eficientes no pior dos casos, ao contrário das árvores de busca binária comuns. ## Balanceamento durante a inserção ### Se o tio é VERMELHO 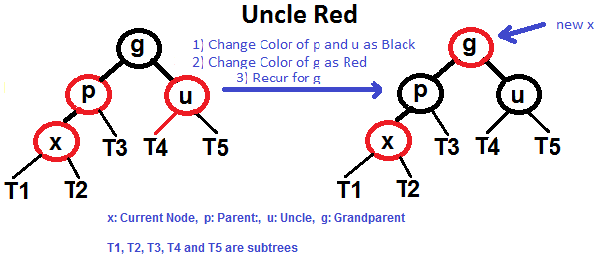 ### Se o tio é PRETO - Caso Esquerda Esquerda (`p` é o filho a esquerda de `g` e `x`, é o filho a esquerda de `p`) - Caso Esquerda Direita (`p` é o filho a esquerda de `g` e `x`, é o filho a direita de `p`) - Caso Direita Direita (`p` é o filho a direita de `g` e `x`, é o filho da direita de `p`) - Caso Direita Esqueda (`p` é o filho a direita de `g` e `x`, é o filho a esquerda de `p`) #### Caso Esquerda Esquerda (Veja g, p e x) 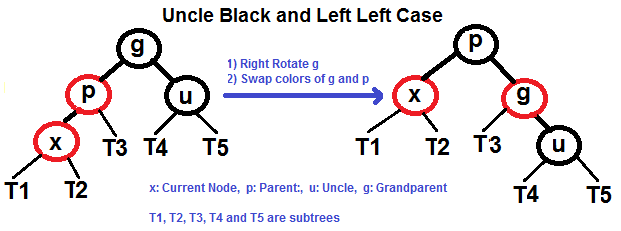 #### Caso Esquerda Direita (Veja g, p e x) 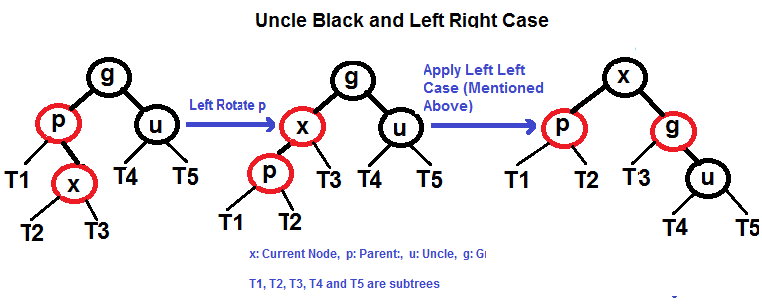 #### Caso Direita Direita (Veja g, p e x) 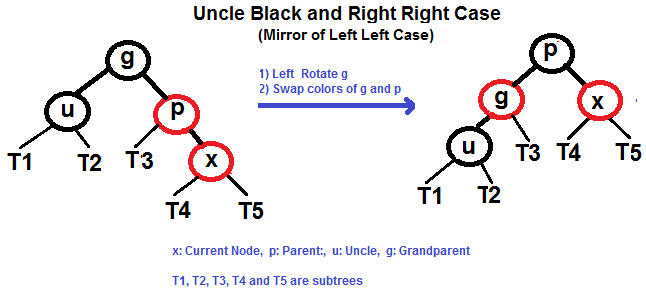 #### Caso Direita Esquerda (Veja g, p e x) 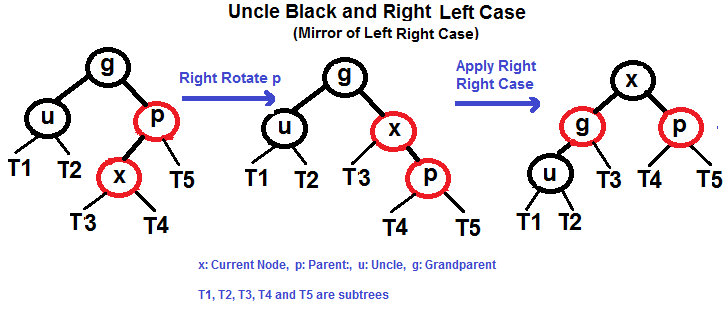 ## Referências - [Wikipedia](https://en.wikipedia.org/wiki/Red%E2%80%93black_tree) - [Red Black Tree Insertion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=UaLIHuR1t8Q&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=63) - [Red Black Tree Deletion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=CTvfzU_uNKE&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=64) - [Red Black Tree Insertion on GeeksForGeeks](https://www.geeksforgeeks.org/red-black-tree-set-2-insert/) - [Red Black Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/RedBlack.html)