TriangularMesh

[OrtnerMichael]

Discussion how the FacetBody class should look like.

TBD

from previous posting:

The FacetBody class

This class should be quite similar to the TriangularMesh class that @Alexboiboi introduced in the original facet branch, but it is still work in progress and features should still be discussed. The idea is that triangular meshes can be handed over easily, that inside-outside checks will be performed by default ( but can be turned off), and that facet orientation is automatically fixed by default (but can also be turned off).

Parameters: magnetization (the usual) and vertices shape (n,3) and triangles shape (n,3)

It seems to be the common choice in defining meshes through a list of unique vertices, and a second list of indices that define the cells. This is done in pyvista, scipy, pymesh, gmesh, ... . Since we already used vertices in other classes I would use this again for the points, and I really like triangles for the index list.

• pymesh.Mesh uses a list of unique vertices called vertices and a list of face index triplets called faces, supporting triangles and quad faces.
• pyvista.PolyData objects use a list of unique vertices called points and a 1D array [3, 1, 2, 3, 3, 2, 3, 4, ...] called faces where the bold number indicates how many indices define the next face. This enables non-triangular meshes.
• scipy.spatial.Delauny uses a list of vertices called points and a list of face index triplets (like PyMesh) called simplices. The points are not unique.

[Alexboiboi]

Current work at https://github.com/magpylib/magpylib/tree/trimesh_body

Tasks

• class naming TriangularMesh
• Object interface
• Field functions
• check getBH (inside/outside)
  • can be deactivated and set explicitly in core for performance (otherwise auto by default)
• body checks (can be deactivated)
  • automatic facets reorienting (opt out)
  • check if mesh is closed (opt out)
  • check if mesh self intersects (opt in) - TriangularMesh - self-intersection check #589
  • check if body is discontinuous (or inside another mesh)
    • e.g. cube inside another cube without intersecting, or two separate cubes
    • may not need to check it, the inside/outside method should be sufficient, @OrtnerMichael thoughts?)
• graphical implementation
  • display TriangularMesh objects
  • Rework the style structure:
    • TriangularMesh inherits from the Magnet family and its style class, if specified defaults can be different for the TriangularMesh classes (use of composition).
    • TriangularMesh also gets Orientation properties, by default show=False
  • display triangles orientations via style.orientation properties
  • display open edges via style.mesh.open.show (+ line and marker properties)
  • display disjoint edges via style.mesh.disjoint.show (+ line and marker properties + color cycling through parts, currently cycle=["red", "blue", "green"])
  • display intersecting edges via style.mesh.intersect.show (+ line and marker properties) - TriangularMesh - self-intersection check #589

Other tasks

• tests
• docstrings (+ examples)
• changelog
• docs with examples

[OrtnerMichael]

@Alexboiboi I played a bit around with TriangularMesh, started to go through your code and here are a few points that we need to discuss before I start changing/implementing anything

Points of Discussion

1. I think the information that defines the TriangularMesh() should be given in two attributes points/vertices [shape (n,3)] denoting unique vertices, and triangles/facets/faces/simplices [shape (m,3), type int] to denote the triangles as is commonly done in various graphic packages and meshers.

   • I would vote for vertices for consistency with other Magpy classes.
   • I would vote for triangles because its most descriptive.

2. Obviously both vertices and triangles are parameters not just attributes.

3. We should consider if the representation in shape (n,3,3), currently termed facets and originally used for the Facet class, should be included at all. I think I'm against it, at best we should provide a method export_faces ... but better not since its just a single numpy command: facets = np.take(vertices, triangles, axis=0).

4. I'm strongly against the use of scipy..ConvexHull(). When a user wants to do that, he should, but that's not our problem and we should really avoid adding "features" that are solved with one-liners, (triangles=ConvexHull(vertices).simplices), especially not when this adds 100 lines to our code !

5. What I think could make sense are functions/methods generate_from_pyvista(PolyData object) to easily import bodies from other libraries such as pyvita, gmesh, matplotlib?, .... but we should discuss which of those features are actually needed and add them accordingly. Specifically, generate_from_pyvista(PolyData object) can be solved with two lines of very simple code

vertices = pv_obj.points
triangles = pv_obj.faces.reshape(-1,4)[:,1:]

what do you think ?

[OrtnerMichael]

And what do you think of this ? 👯‍♂️

[OrtnerMichael]

Discussion @OrtnerMichael and @Alexboiboi :

1. Facets out
2. vertices and triangles should be attributes without setters !
3. import from other libraries using class methods TBD
   a. from_pyvista given a pyvista PolyData object
   b. from_points given points and using scipy..ConvexHull

Checks

• closed mesh (validate mesh)
• self intersection (includes 0-volume / planar bodies and non-orientable bodies)
• triangle orientation
• separate bodies (do we want this ? if yes how ?)

Graphics

• defaults / style family / composition ?
• orientation default should be False, contrary as Triangle
• show mesh problems (open parts, intersecting triangles)

[Alexboiboi]

Hi @OrtnerMichael,

The changes I could implement are now up to date with test (100% coverage). Waiting for feedback.

The styling topic is mostly independent, and I'll continue to work on in in another branch

[OrtnerMichael]

@Alexboiboi

Looks great - everything works as discussed !
Also i like the classmethods of TriangularMesh

import pyvista as pv
import magpylib as magpy
magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(1,2,3),
    polydata=pv.Text3D("I'm loving it")
).show(backend='pyvista')

I'll check and work on the methods face_flip, inside_outside, closed_mesh, separate_bodies, and also to clean up e.g. checks that are in the TriangularMesh class ... not sure if they should be there... and maybe start working on the docstrings.

[Alexboiboi]

Hi @OrtnerMichael ,

I have updated the style structure to allow for composition. The TriangularMesh object can now define its own defaults and fall back to the Magnet style. I added some mesh visualization features such as open and disjoint properties (see examples below).

Can you check it out?

import magpylib as magpy
import pyvista as pv

trimesh = magpy.magnet.TriangularMesh.from_pyvista(magnetization=(0, 0, 1000),polydata=pv.Cube())
trimesh._triangles = trimesh.triangles[1:]  # open the mesh
trimesh.show(backend="plotly")

import magpylib as magpy
import pyvista as pv
import numpy as np
mag = (111, 222, 33)
disjoint_mesh = magpy.magnet.TriangularMesh.from_pyvista(mag, pv.Text3D("ABC"))
disjoint_mesh.show(backend="plotly")

[Alexboiboi]

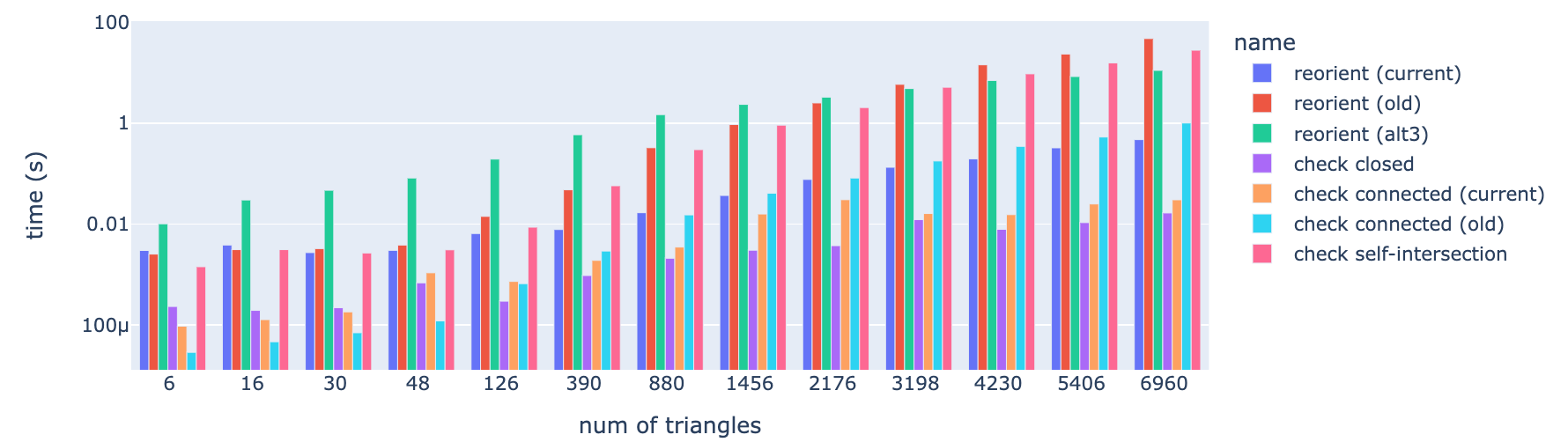
Hi @OrtnerMichael,

I have done some basic profiling of the implemented mesh validation algorithms (also including self-intersection).
In short, the reorientation of facets was by far the most time consuming operation when having lots of facets (self-intersection is in the same order). I replaced it with a more efficient one (current, can probably still be improved)

log scale

linear scale

To reproduce

from time import perf_counter

import magpylib as magpy
import numpy as np
import pandas as pd
import plotly.express as px
import pyvista as pv
from magpylib._src.fields.field_BH_triangularmesh import (
    fix_trimesh_orientation,
    get_disjoint_triangles_subsets,
    lines_end_in_trimesh,
    mask_inside_trimesh,
    trimesh_is_closed,
    v_norm_cross,
)

def trimesh_is_connected_old(triangles: np.ndarray) -> np.ndarray:
    """
    Check if triangular mesh consists of multiple disconnected parts.

    Input: triangles: np.ndarray, shape (n,3), dtype int
        triples of indices

    Output: bool (True if connected, False if disconnected)
    """
    tri_list = triangles.tolist()
    connected = [np.min(triangles)]

    # start with lowest index
    # cycle through tri_list and unique-add indices from connecting triangles
    # when adding indices to connected, remove respective triangle from tri_list
    # After completing a cycle, check if a new triangle was added
    # if not, and tri_list still contains some triangles, then these faces must be
    # disconnected from the rest
    added_new = True
    while added_new:
        added_new = False
        # cycle through all triangles that are not connected yet
        for tria in tri_list:
            for ii in tria:
                if ii in connected:
                    # add new triangle to connected
                    for iii in tria:
                        if iii not in connected:
                            connected.append(iii)
                    tri_list.remove(tria)
                    added_new = True
                    break
    if tri_list:
        return False
    return True

def fix_trimesh_orientation_old(vertices: np.ndarray, triangles: np.ndarray) -> np.ndarray:
    """
    Check if all triangles are oriented outwards. Fix the ones that are not, and return an
    array of properly oriented triangles.

    Parameters
    ----------
    vertices: np.ndarray, shape (n,3)
        vertices of the mesh

    triangles: np.ndarray, shape (n,3), dtype int
        triples of indices

    Returns
    -------
    triangles: np.ndarray, shape (n,3), dtype int
        fixed triangles

    """
    facets = vertices[triangles]

    # compute facet orientations (normalized)
    a = facets[:, 0, :] - facets[:, 1, :]
    b = facets[:, 1, :] - facets[:, 2, :]
    orient = v_norm_cross(a, b)

    # create check points by displacing the facet center in facet orientation direction
    eps = 1e-6  # unfortunately this must be quite a large number :(
    facet_center = facets.mean(axis=1)
    check_points = facet_center + orient * eps

    # find points which are now inside
    inside_mask = mask_inside_trimesh(check_points, facets)

    # flip triangles which point inside
    triangles[inside_mask] = triangles[inside_mask][:, [0, 2, 1]]
    return triangles

def fix_trimesh_orientation2(vertices: np.ndarray, triangles: np.ndarray) -> np.ndarray:
    """
    Check if all triangles are oriented outwards. Fix the ones that are not, and return an
    array of properly oriented triangles.

    Parameters
    ----------
    vertices: np.ndarray, shape (n,3)
        vertices of the mesh

    triangles: np.ndarray, shape (n,3), dtype int
        triples of indices

    Returns
    -------
    triangles: np.ndarray, shape (n,3), dtype int
        fixed triangles

    """
    facets = vertices[triangles]

    # compute facet orientations (normalized)
    a = facets[:, 0, :] - facets[:, 1, :]
    b = facets[:, 1, :] - facets[:, 2, :]
    orient = v_norm_cross(a, b)

    # create check points by displacing the facet center in facet orientation direction
    eps = 1e-2  # unfortunately this must be quite a large number :(
    facet_center = facets.mean(axis=1)
    check_points = facet_center + orient * eps
    check_points += b * eps  # avoid test_line to cross edge
    # create test-lines from outside to test-points
    facets_mins = np.min(facets, axis=1)
    facets_maxes = np.max(facets, axis=1)
    for ind, _ in enumerate(triangles):
        facet_min, facet_max = facets_mins[ind], facets_maxes[ind]
        coords = np.array([0, 1, 2])
        first_non_zero_coord = coords[orient[ind] != 0][0]
        coords = np.delete(coords, first_non_zero_coord)
        pt = check_points[ind]
        line = np.array([pt, pt])
        line[0, first_non_zero_coord] = facet_min[first_non_zero_coord] - 1

        mask_min1 = (facet_min[coords[0]] <= facets_mins[:, coords[0]]) & (
            facets_mins[:, coords[0]] <= facet_max[coords[0]]
        )
        mask_max1 = (facet_min[coords[0]] <= facets_maxes[:, coords[0]]) & (
            facets_maxes[:, coords[0]] <= facet_max[coords[0]]
        )
        mask_min2 = (facet_min[coords[1]] <= facets_mins[:, coords[1]]) & (
            facets_mins[:, coords[1]] <= facet_max[coords[1]]
        )
        mask_max2 = (facet_min[coords[1]] <= facets_maxes[:, coords[1]]) & (
            facets_maxes[:, coords[1]] <= facet_max[coords[1]]
        )
        mask = (mask_min1 | mask_max1) & (mask_min2 | mask_max2)
        if lines_end_in_trimesh(np.array([line]), facets[mask])[0]:
            triangles[ind] = triangles[ind][[0, 2, 1]]
    return triangles


def signed_volume(a, b, c, d):
    """Computes the signed volume of a series of tetrahedrons defined by the vertices in
    a, b c and d. The ouput is an SxT array which gives the signed volume of the tetrahedron
    defined by the line segment 's' and two vertices of the triangle 't'."""

    return np.sum((a - d) * np.cross(b - d, c - d), axis=2)


def segments_intersect_triangle(segments, facets, summation=True):
    """For each line segment in `segments`, this function computes how many times it intersects
    any of the facets given in `facets`.

    Parameters
    ----------
    segments: Sx2x3 array
        Array of `S` line segments where the first index specifies the S^th line segment, the
        second index refers to the start or end point of the segment, and the third index points
        to the x, y, z coordinates of the line segment point.

    facets: Tx3x3
        Array of `T` triangular facets, where the first index specifies the T^th triangle, the
        second index refers to one of the three vertices (which don't have to be in any particular
        order), and the third index points to the x,y,z coordinates the the triangle vertex.

    summation: bool, optional
        If `True`, a binary array is return which only tells if the S^th line segment intersects
        any of  the facets given. If `False`, returns a SxT array that tells which facets are
        intersected.

    Returns
    -------
        If `'summation'` is `True`, returns a binary array of size S which tells whether the S^th
        line segment intersects any of the facets given. Otherwise returns a SxT array that tells
        which facets are intersected.
    """

    s, t = segments, facets
    # compute the normals to each triangle
    normals = np.cross(t[:, 2] - t[:, 0], t[:, 2] - t[:, 1])
    normals /= np.linalg.norm(normals, axis=1, keepdims=True)

    # get sign of each segment endpoint, if the sign changes then we know this segment crosses the
    # plane which contains a triangle. If the value is zero the endpoint of the segment lies on the
    # plane.
    s0, s1 = s[:, :1], s[:, 1:]  # -> S x T x 3 arrays
    sign1 = np.sign(np.sum(normals * (s0 - t[:, 2]), axis=2))  # S x T
    sign2 = np.sign(np.sum(normals * (s1 - t[:, 2]), axis=2))  # S x T

    # determine segments which cross the plane of a triangle.
    #  -> 1 if the sign of the end points of s is
    # different AND one of end points of s is not a vertex of t
    cross = (sign1 != sign2) * (sign1 != 0) * (sign2 != 0)  # S x T

    # get signed volumes
    v = [
        np.sign(signed_volume(t[:, i], t[:, j], s0, s1))
        for i, j in zip((0, 1, 2), (1, 2, 0))
    ]  # S x T
    same_volume = np.logical_and(
        (v[0] == v[1]), (v[1] == v[2])
    )  # 1 if s and t have same sign in v0, v1 and v2

    res = cross * same_volume
    if summation:
        res = np.sum(res, axis=1)

    return res


def check_self_intersection(triangles):
    edges = np.concatenate(
        [triangles[:, 0:2], triangles[:, 1:3], triangles[:, ::2]], axis=0
    )
    edges_uniq, edges_counts = np.unique(
        np.sort(edges, axis=1), axis=0, return_counts=True
    )
    facets = vertices[triangles]
    segments = vertices[edges_uniq]
    return segments_intersect_triangle(segments, facets)


def time_it(func, *args, **kwargs):
    start = perf_counter()
    func(*args, **kwargs)
    return perf_counter() - start

inputs = {
    "reorient (current)": {"func": fix_trimesh_orientation, "names": ("vertices", "triangles")},
    "reorient (old)": {"func": fix_trimesh_orientation_old, "names": ("vertices", "triangles")},
    "reorient (alt3)": {"func": fix_trimesh_orientation2, "names": ("vertices", "triangles")},
    "check closed": {"func": trimesh_is_closed, "names": ("triangles",)},
    "check connected (current)": {"func": get_disjoint_triangles_subsets, "names": ("triangles", )},
    "check connected (old)": {"func": trimesh_is_connected_old, "names": ("triangles", )},
    "check self-intersection": {"func": check_self_intersection, "names": ("triangles")},
}
results=[]
tri = []
for resol in [ 3, 4, 5, 6, 9, 15, 22, 28, 34, 41, 47, 53, 60]:
    resol = int(resol)
    polydata = pv.Sphere(phi_resolution=resol, theta_resolution=resol).triangulate()
    vertices = polydata.points
    triangles = polydata.faces.reshape(-1, 4)[:, 1:]
    print(f"batch with {len(triangles)} triangles")
    kwargs = {"triangles": triangles, "vertices": vertices}
    for name, val in inputs.items():
        t = time_it(val["func"], **{k:v for k,v in kwargs.items() if k in val["names"]})
        res = {"name": name, "time": t, "triangles": len(triangles)}
        print(res)
        results.append(res)

df = pd.DataFrame(results)

df["num of triangles"] = df["triangles"].astype(str) + " "

fig = px.bar(
    df,
    x="num of triangles",
    y="time",
    # facet_col="variable",
    color="name",
    labels={"time": "time (s)"},
    #log_x=True,
    log_y=True,
    facet_col_spacing=0.05,
    barmode="group",
)
fig.update_yaxes(showticklabels=True)
fig.show()

fig.update_layout( yaxis_type="linear")
fig.show()

[Alexboiboi]

Importing from pyvista leads most of the time to invalid meshes. Especially when performing boolean operations, which is a bumer :( (maybe worth opening a github issue in their repo). It don't see a straightforward solution to this, since we are only performing mesh validation. The only fix performed within magpylib is the reorientation of triangles and we will certainly not start to implement mesh repairing tools within magpylib. We could try with other meshing libraries how boolean operation perform and include some example(s) in the docs if it works well. We could even keep a bad example in the docs for info (see below).

@OrtnerMichael any thoughts?

import pyvista as pv
import magpylib as magpy

# create a complex pyvista PolyData object
sphere = pv.Sphere(radius=0.85)
dodec = pv.Dodecahedron().triangulate()
obj = dodec.boolean_difference(sphere)

magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(0,0,100),
    polydata=obj,
    validate_connected=False,
    validate_closed=False,
    reorient_triangles=False,
    style_label="Dodecahedron cut by Sphere",
)

magnet.show(backend='plotly')

import magpylib as magpy
import pyvista as pv

# create a complex pyvista PolyData object
cyl = pv.Cylinder(radius=0.4, height=2).triangulate()
cyl = cyl.rotate_y(-30)
dodec = pv.Dodecahedron().triangulate()
obj = dodec.boolean_difference(cyl)
magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(0, 0, 100),
    polydata=obj,
    validate_connected=False,
    validate_closed=False,
    reorient_triangles=False,
    style_label="Dodecahedron cut by Cylinder",
)

magnet.show(backend="plotly")

import magpylib as magpy
import pyvista as pv

# create a complex pyvista PolyData object
cube = pv.Cube(x_length=0.5, y_length=0.5, z_length=3).triangulate()
cube = cube.rotate_x(30)
dodec = pv.Dodecahedron().triangulate()
obj = dodec.boolean_difference(cube)
magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(0, 0, 100),
    polydata=obj,
    validate_connected=False,
    validate_closed=False,
    reorient_triangles=False,
    style_label="Dodecahedron cut by Cuboid",
)

magnet.show(backend="plotly")

[Alexboiboi]

Should we add a method to_collection to distribute disjoint parts into children of a collection? What do you think?

[Alexboiboi]

With the help of the .clean() method it is possible to get rid of the "disconnected" problem, but the mesh remains open...

import pyvista as pv
import magpylib as magpy

# create a complex pyvista PolyData object
sphere = pv.Sphere(radius=0.85)
dodec = pv.Dodecahedron().triangulate()
obj = dodec.boolean_difference(sphere)
obj = obj.clean()
magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(0,0,100),
    polydata=obj,
    validate_connected=False,
    validate_closed=False,
    reorient_triangles=False,
    style_label="Dodecahedron cut by Sphere",
)

magnet.show(backend='plotly')

import magpylib as magpy
import pyvista as pv

# create a complex pyvista PolyData object
cyl = pv.Cylinder(radius=0.4, height=2).triangulate()
cyl = cyl.rotate_y(-30)
dodec = pv.Dodecahedron().triangulate()
obj = dodec.boolean_difference(cyl)
obj = obj.clean()
magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(0, 0, 100),
    polydata=obj,
    validate_connected=False,
    validate_closed=False,
    reorient_triangles=False,
    style_label="Dodecahedron cut by Cylinder",
)

magnet.show(backend="plotly")

import magpylib as magpy
import pyvista as pv

# create a complex pyvista PolyData object
cube = pv.Cube(x_length=0.5, y_length=0.5, z_length=3).triangulate()
cube = cube.rotate_x(30)
dodec = pv.Dodecahedron().triangulate()
obj = dodec.boolean_difference(cube)
obj = obj.clean()
magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(0, 0, 100),
    polydata=obj,
    validate_connected=False,
    validate_closed=False,
    reorient_triangles=False,
    style_label="Dodecahedron cut by Cuboid",
)

magnet.show(backend="plotly")

[Alexboiboi]

And with the .subdivide() method applied to the dodecahedron it makes a clean mesh ;)

import pyvista as pv
import magpylib as magpy

# create a complex pyvista PolyData object
sphere = pv.Sphere(radius=0.85)
dodec = pv.Dodecahedron().triangulate().subdivide(2)
obj = dodec.boolean_difference(sphere)
obj = obj.clean()
magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(0,0,100),
    polydata=obj,
    style_label="Dodecahedron cut by Sphere",
)

magnet.show(backend='plotly')

import magpylib as magpy
import pyvista as pv

# create a complex pyvista PolyData object
cyl = pv.Cylinder(radius=0.4, height=2).triangulate()
cyl = cyl.rotate_y(-30)
dodec = pv.Dodecahedron().triangulate().subdivide(2)
obj = dodec.boolean_difference(cyl)
obj = obj.clean()
magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(0, 0, 100),
    polydata=obj,
    style_label="Dodecahedron cut by Cylinder",
)

magnet.show(backend="plotly")

import magpylib as magpy
import pyvista as pv

# create a complex pyvista PolyData object
cube = pv.Cube(x_length=0.5, y_length=0.5, z_length=3).triangulate()
cube = cube.rotate_x(30)
dodec = pv.Dodecahedron().triangulate().subdivide(2)
obj = dodec.boolean_difference(cube)
obj = obj.clean()
magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=(0, 0, 100),
    polydata=obj,
    style_label="Dodecahedron cut by Cuboid",
)

magnet.show(backend="plotly")

[OrtnerMichael]

hi @Alexboiboi

1. Great that you managed to improve the algorithms ! Feel free to replace your/my old ones any time.
2. Concerning pyvista meshes from boolean operations: this looks like a lot of good and important know-how that should go to the documentation !

Do you see any other problems when creating complex shapes with pyvista ?

Can I review the trimesh body branch ?

[Alexboiboi]

U can review the branch, I may just edit som visualization features

[Alexboiboi]

To summarize the current validation performance:
With 10^4 triangles, validation takes approx 1 sec.

from time import perf_counter

import magpylib as magpy
import numpy as np
import pandas as pd
import plotly.express as px
import pyvista as pv
from magpylib._src.fields.field_BH_triangularmesh import (
    fix_trimesh_orientation,
    get_disjoint_triangles_subsets,
    trimesh_is_closed,
)


def time_it(func, *args, **kwargs):
    start = perf_counter()
    func(*args, **kwargs)
    return perf_counter() - start

inputs = {
    "reorient": {"func": fix_trimesh_orientation, "names": ("vertices", "triangles")},
    "validate closed": {"func": trimesh_is_closed, "names": ("triangles",)},
    "validate connected": {"func": get_disjoint_triangles_subsets, "names": ("triangles", )},
}
results=[]
tri = []
for resol in [ 3, 4, 5, 6, 9, 15, 22, 28, 34, 41, 47, 53, 60, 67, 75]:
    resol = int(resol)
    polydata = pv.Sphere(phi_resolution=resol, theta_resolution=resol).triangulate()
    vertices = polydata.points
    triangles = polydata.faces.reshape(-1, 4)[:, 1:]
    print(f"batch with {len(triangles)} triangles")
    kwargs = {"triangles": triangles, "vertices": vertices}
    for name, val in inputs.items():
        t = time_it(val["func"], **{k:v for k,v in kwargs.items() if k in val["names"]})
        res = {"name": name, "time": t, "triangles": len(triangles)}
        print(res)
        results.append(res)

df = pd.DataFrame(results)

df["num of triangles"] = df["triangles"].astype(str) + " "
df["time [ms]"] = df["time"]*1000
fig = px.bar(
    df,
    x="num of triangles",
    y="time [ms]",
    # facet_col="variable",
    color="name",
    #log_x=True,
    log_y=True,
    facet_col_spacing=0.05,
    barmode="stack", # ['stack', 'group', 'overlay', 'relative']
)
fig.show()

[Alexboiboi]

Gained again almost a factor 10 by optimizing triangle reorientation. Now it takes approx 1 sec for 50k elements.

log scale

linear scale

[Alexboiboi]

to test some memory issue:

• see Abnormal memory usage when working with large object collections #600

import magpylib as magpy
import matplotlib.pyplot as plt
import numpy as np
import pyvista as pv

Nt = 10000 # target number of triangles
r = int(np.sqrt(Nt/2))
sphere  = pv.Sphere(theta_resolution=r, phi_resolution=r)
magnet = magpy.magnet.TriangularMesh.from_pyvista(
    magnetization=[0, 100, 0],
    polydata = sphere,
)

N = 30
xs = np.linspace(-1e3, 1e3, N)
ys = np.linspace(0, 1e3, N)
grid = np.array([[(x, y, 0) for x in xs] for y in ys])

%%time

Np = np.prod(grid.shape[:-1]) # number of points
Ns = 100  # number of subsets
slices = [slice(i * Np // Ns, (i + 1) * Np // Ns) for i in range(Ns)]

B = np.concatenate(
    [magpy.getB(magnet, grid.reshape(-1,3)[sl]) for sl in slices]
).reshape(grid.shape)

%%time

B1 = magpy.getB(magnet, grid)

np.testing.assert_allclose(B, B1)

[OrtnerMichael]

this is completed with #598