# Euclidean algorithm In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two numbers, the largest number that divides both of them without leaving a remainder. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, `21` is the GCD of `252` and `105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same number `21` is also the GCD of `105` and `252 − 105 = 147`. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, they are the GCD of the original two numbers. By reversing the steps, the GCD can be expressed as a sum of the two original numbers each multiplied by a positive or negative integer, e.g., `21 = 5 × 105 + (−2) × 252`. The fact that the GCD can always be expressed in this way is known as Bézout's identity. 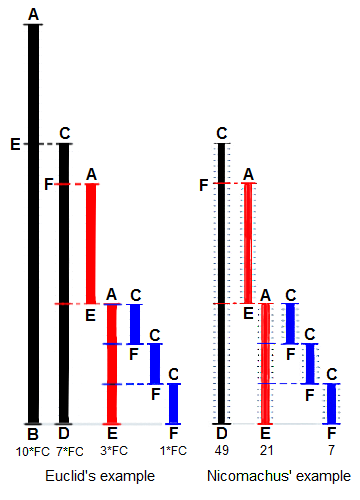 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths `BA` and `DC`, both defined to be multiples of a common "unit" length. The length `DC` being shorter, it is used to "measure" `BA`, but only once because remainder `EA` is less than `DC`. EA now measures (twice) the shorter length `DC`, with remainder `FC` shorter than `EA`. Then `FC` measures (three times) length `EA`. Because there is no remainder, the process ends with `FC` being the `GCD`. On the right Nicomachus' example with numbers `49` and `21` resulting in their GCD of `7` (derived from Heath 1908:300).  A `24-by-60` rectangle is covered with ten `12-by-12` square tiles, where `12` is the GCD of `24` and `60`. More generally, an `a-by-b` rectangle can be covered with square tiles of side-length `c` only if `c` is a common divisor of `a` and `b`.  Subtraction-based animation of the Euclidean algorithm. The initial rectangle has dimensions `a = 1071` and `b = 462`. Squares of size `462×462` are placed within it leaving a `462×147` rectangle. This rectangle is tiled with `147×147` squares until a `21×147` rectangle is left, which in turn is tiled with `21×21` squares, leaving no uncovered area. The smallest square size, `21`, is the GCD of `1071` and `462`. ## References [Wikipedia](https://en.wikipedia.org/wiki/Euclidean_algorithm)