|
| 1 | +# Euclidean algorithm |
| 2 | + |
| 3 | +In mathematics, the Euclidean algorithm, or Euclid's algorithm, |
| 4 | +is an efficient method for computing the greatest common divisor |
| 5 | +(GCD) of two numbers, the largest number that divides both of |
| 6 | +them without leaving a remainder. |
| 7 | + |
| 8 | +The Euclidean algorithm is based on the principle that the |
| 9 | +greatest common divisor of two numbers does not change if |
| 10 | +the larger number is replaced by its difference with the |
| 11 | +smaller number. For example, `21` is the GCD of `252` and |
| 12 | +`105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same |
| 13 | +number `21` is also the GCD of `105` and `252 − 105 = 147`. |
| 14 | +Since this replacement reduces the larger of the two numbers, |
| 15 | +repeating this process gives successively smaller pairs of |
| 16 | +numbers until the two numbers become equal. |
| 17 | +When that occurs, they are the GCD of the original two numbers. |
| 18 | + |
| 19 | +By reversing the steps, the GCD can be expressed as a sum of |
| 20 | +the two original numbers each multiplied by a positive or |
| 21 | +negative integer, e.g., `21 = 5 × 105 + (−2) × 252`. |
| 22 | +The fact that the GCD can always be expressed in this way is |
| 23 | +known as Bézout's identity. |
| 24 | + |
| 25 | +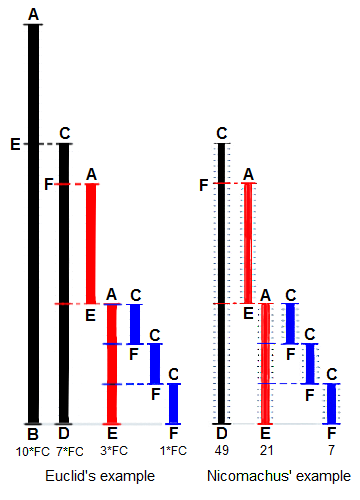 |
| 26 | + |
| 27 | +Euclid's method for finding the greatest common divisor (GCD) |
| 28 | +of two starting lengths `BA` and `DC`, both defined to be |
| 29 | +multiples of a common "unit" length. The length `DC` being |
| 30 | +shorter, it is used to "measure" `BA`, but only once because |
| 31 | +remainder `EA` is less than `DC`. EA now measures (twice) |
| 32 | +the shorter length `DC`, with remainder `FC` shorter than `EA`. |
| 33 | +Then `FC` measures (three times) length `EA`. Because there is |
| 34 | +no remainder, the process ends with `FC` being the `GCD`. |
| 35 | +On the right Nicomachus' example with numbers `49` and `21` |
| 36 | +resulting in their GCD of `7` (derived from Heath 1908:300). |
| 37 | + |
| 38 | + |
| 39 | + |
| 40 | +A `24-by-60` rectangle is covered with ten `12-by-12` square |
| 41 | +tiles, where `12` is the GCD of `24` and `60`. More generally, |
| 42 | +an `a-by-b` rectangle can be covered with square tiles of |
| 43 | +side-length `c` only if `c` is a common divisor of `a` and `b`. |
| 44 | + |
| 45 | + |
| 46 | + |
| 47 | +Subtraction-based animation of the Euclidean algorithm. |
| 48 | +The initial rectangle has dimensions `a = 1071` and `b = 462`. |
| 49 | +Squares of size `462×462` are placed within it leaving a |
| 50 | +`462×147` rectangle. This rectangle is tiled with `147×147` |
| 51 | +squares until a `21×147` rectangle is left, which in turn is |
| 52 | +tiled with `21×21` squares, leaving no uncovered area. |
| 53 | +The smallest square size, `21`, is the GCD of `1071` and `462`. |
| 54 | + |
| 55 | +## References |
| 56 | + |
| 57 | +[Wikipedia](https://en.wikipedia.org/wiki/Euclidean_algorithm) |
0 commit comments