# Red–Black Tree A **red–black tree** is a kind of self-balancing binary search tree in computer science. Each node of the binary tree has an extra bit, and that bit is often interpreted as the color (red or black) of the node. These color bits are used to ensure the tree remains approximately balanced during insertions and deletions. Balance is preserved by painting each node of the tree with one of two colors in a way that satisfies certain properties, which collectively constrain how unbalanced the tree can become in the worst case. When the tree is modified, the new tree is subsequently rearranged and repainted to restore the coloring properties. The properties are designed in such a way that this rearranging and recoloring can be performed efficiently. The balancing of the tree is not perfect, but it is good enough to allow it to guarantee searching in `O(log n)` time, where `n` is the total number of elements in the tree. The insertion and deletion operations, along with the tree rearrangement and recoloring, are also performed in `O(log n)` time. An example of a red–black tree:  ## Properties In addition to the requirements imposed on a binary search tree the following must be satisfied by a red–black tree: - Each node is either red or black. - The root is black. This rule is sometimes omitted. Since the root can always be changed from red to black, but not necessarily vice versa, this rule has little effect on analysis. - All leaves (NIL) are black. - If a node is red, then both its children are black. - Every path from a given node to any of its descendant NIL nodes contains the same number of black nodes. Some definitions: the number of black nodes from the root to a node is the node's **black depth**; the uniform number of black nodes in all paths from root to the leaves is called the **black-height** of the red–black tree. These constraints enforce a critical property of red–black trees: _the path from the root to the farthest leaf is no more than twice as long as the path from the root to the nearest leaf_. The result is that the tree is roughly height-balanced. Since operations such as inserting, deleting, and finding values require worst-case time proportional to the height of the tree, this theoretical upper bound on the height allows red–black trees to be efficient in the worst case, unlike ordinary binary search trees. ## Balancing during insertion ### If uncle is RED 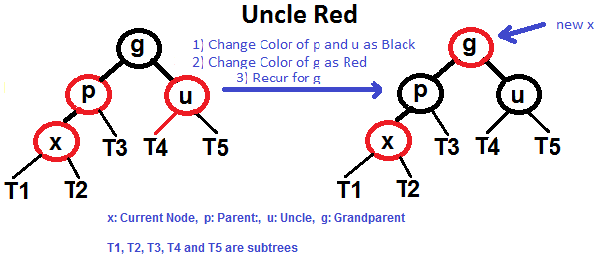 ### If uncle is BLACK - Left Left Case (`p` is left child of `g` and `x` is left child of `p`) - Left Right Case (`p` is left child of `g` and `x` is right child of `p`) - Right Right Case (`p` is right child of `g` and `x` is right child of `p`) - Right Left Case (`p` is right child of `g` and `x` is left child of `p`) #### Left Left Case (See g, p and x) 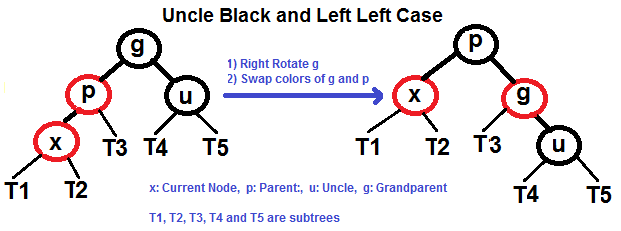 #### Left Right Case (See g, p and x) 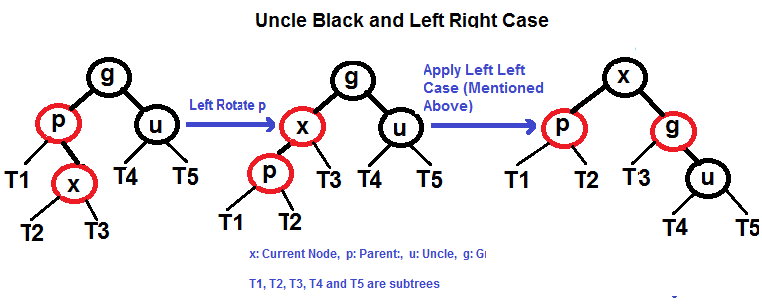 #### Right Right Case (See g, p and x) 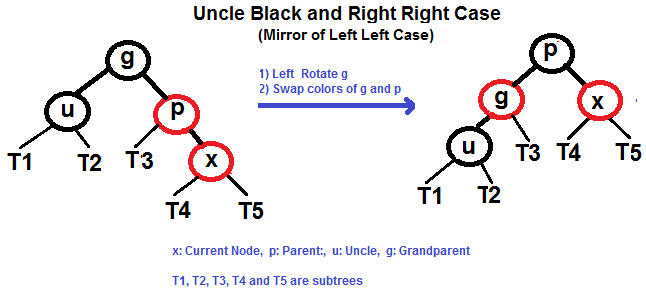 #### Right Left Case (See g, p and x) 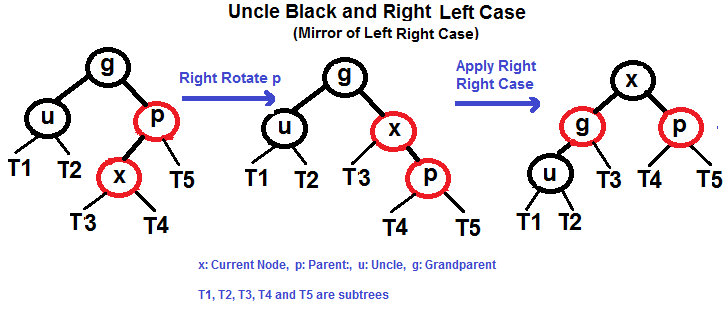 ## References - [Wikipedia](https://en.wikipedia.org/wiki/Red%E2%80%93black_tree) - [Red Black Tree Insertion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=UaLIHuR1t8Q&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=63) - [Red Black Tree Deletion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=CTvfzU_uNKE&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=64) - [Red Black Tree Insertion on GeeksForGeeks](https://www.geeksforgeeks.org/red-black-tree-set-2-insert/) - [Red Black Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/RedBlack.html)